
 一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )
一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | $\frac{1+\sqrt{2}}{3}$ |
分析 根据题意和三视图画出直观图,由正方体的性质求出截去三棱锥的棱长,由三棱锥P-ABC的体积相等和题意列出方程,化简后即可得到答案.
解答 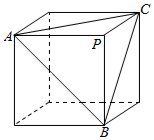 解:根据题意和三视图画出直观图,其中三棱锥P-ABC是截去的一角,
解:根据题意和三视图画出直观图,其中三棱锥P-ABC是截去的一角,
∵三视图中的三个四边形都是边长为2的正方形,
∴正方体的棱长等于2,则AB=AC=BC=$2\sqrt{2}$,
则△ABC的面积是$\frac{1}{2}×2\sqrt{2}×2\sqrt{2}×\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
由三棱锥P-ABC的体积相等和题意得,$\frac{1}{3}×2\sqrt{3}×h=\frac{1}{3}×(3×\frac{1}{2}×2×2+2\sqrt{3})×R$,
化简得,$\frac{h}{R}$=$\frac{6+2\sqrt{3}}{2\sqrt{3}}$=$\sqrt{3}+1$,
故选:C.
点评 本题考查几何体三视图的应用,利用等体积法求正三棱锥的高、内切球半径问题,考查空间想象能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD,底面ABCD为菱形,△PAB是等边三角形,∠ABC=60°,AB=2,PC=$\sqrt{6}$
已知四棱锥P-ABCD,底面ABCD为菱形,△PAB是等边三角形,∠ABC=60°,AB=2,PC=$\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°
已知如图,△ABC和△DBC所在的平面互相垂直,且AB=BC=BD=1,∠ABC=∠DBC=120°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
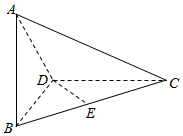 如图,已知三棱锥A-BCD中,DB=DC=BA=2,BD⊥DC,AB⊥平面BCD,E为BC的中点.
如图,已知三棱锥A-BCD中,DB=DC=BA=2,BD⊥DC,AB⊥平面BCD,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(-1,$\frac{1}{3}$).过椭圆E内一点P(1,$\frac{1}{2}$)的两条直线分别与椭圆交于点A、C和B、D,且满足$\overrightarrow{AP}$=λ$\overrightarrow{PC}$,$\overrightarrow{BP}$=λ$\overrightarrow{PD}$,其中λ为实数.当直线AP平行于x轴时,对应的λ=$\frac{1}{5}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(-1,$\frac{1}{3}$).过椭圆E内一点P(1,$\frac{1}{2}$)的两条直线分别与椭圆交于点A、C和B、D,且满足$\overrightarrow{AP}$=λ$\overrightarrow{PC}$,$\overrightarrow{BP}$=λ$\overrightarrow{PD}$,其中λ为实数.当直线AP平行于x轴时,对应的λ=$\frac{1}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )
如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )| A. | 28π | B. | 32π | C. | 16π | D. | 12π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com