
【题目】求下列方程组的解集:
(1)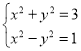 ;(2)
;(2)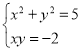 ;(3)
;(3)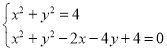 ;(4)
;(4)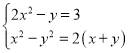 .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)利用加减消元法可求出原方程组的解集;
(2)利用完全平方公式求出![]() 和
和![]() 的值,然后联立方程组,可求出原方程组的解集;
的值,然后联立方程组,可求出原方程组的解集;
(3)将两式相减可得出![]() ,可得
,可得![]() ,代入
,代入![]() ,利用代入消元法可求出原方程组的解集;
,利用代入消元法可求出原方程组的解集;
(4)由![]() 可得
可得![]() 或
或![]() ,由此可得出两个方程组
,由此可得出两个方程组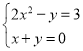 和
和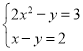 ,利用代入消元法解出这两个方程组,解出即得原方程组的解集.
,利用代入消元法解出这两个方程组,解出即得原方程组的解集.
(1)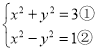 ,
,
①![]() ②得
②得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
①![]() ②得
②得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
因此,原方程组的解集为![]() ;
;
(2)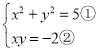 ,
,
①![]() ②
②![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() 或
或![]() ,
,
①![]() ②
②![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() 或
或![]() .
.
所以![]() 或
或![]() 或
或![]() 或
或![]() ,
,
解得![]() 或
或![]() 或
或![]() 或
或![]() ,
,
因此,原方程组的解集为![]() ;
;
(3)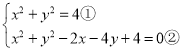 ,
,
①![]() ②得
②得![]() ,即
,即![]() ,可得
,可得![]() ,③,
,③,
将③代入①得![]() ,整理得
,整理得![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此,原方程组的解集为![]() ;
;
(4)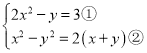 ,
,
由②得![]() ,所以
,所以![]() 或
或![]() ,
,
所以原方程组化为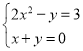 或
或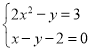 .
.
先解方程组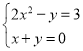 ,由
,由![]() 得
得![]() ,代入
,代入![]() 得
得![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
然后解方程组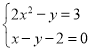 ,由
,由![]() ,得
,得![]() ,代入
,代入![]() 得
得![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此,原方程组的解集为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数,
为参数, ![]() ). 以坐标原点为极点,
). 以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动点,当
上的一个动点,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上所有的点均在直线
上所有的点均在直线![]() 的右下方,求
的右下方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·贵阳第二次联考)在△ABC中,角A,B,C的对边分别为a,b,c,向量m=(a+b,sin A-sin C),向量n=(c,sin A-sin B),且m∥n.
(1)求角B的大小;
(2)设BC的中点为D,且AD=![]() ,求a+2c的最大值及此时△ABC的面积.
,求a+2c的最大值及此时△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包店随机收集了面包种类的有关数据,经分类整理得到下表:
面包类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
面包个数 | 90 | 60 | 30 | 80 | 100 | 40 |
好评率 | 0.6 | 0.45 | 0.7 | 0.35 | 0.6 | 0.5 |
好评率是指:一类面包中获得好评的个数与该类面包的个数的比值.
(1)从面包店收集的面包中随机选取1个,求这个面包是获得好评的第五类面包的概率;
(2)从面包店收集的面包中随机选取1个,估计这个面包没有获得好评的概率;
(3)面包店为增加利润,拟改变生产策略,这将导致不同类型面包的好评率发生变化.假设表格中只有两类面包的好评率数据发生变化,那么哪类面包的好评率增加0.1,哪类面包的好评率减少0.1,使得获得好评的面包总数与样本中的面包总数的比值达到最大?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且tan∠EAB=![]() .
.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD⊥平面ADE;
(3)在CD上是否存在一点M,使得MO∥平面ADE,证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com