
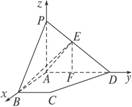
(1)求证:BE⊥PD;
(2)求异面直线AE与CD所成角的大小.(用反三角函数表示)
分析:求一对异面直线所成的角,一是按定义平移转化为两相交直线的夹角;二是在异面直线上各取两个向量,转化为两向量的夹角或补角.
(1)证明:因为PA⊥平面ABCD,所以PA⊥AB.
再由AB⊥AD,得AB⊥平面PAD.
所以AB⊥PD.
又因为AE⊥PD,
所以PD⊥平面ABE.
故BE⊥PD.
(2)解:如图所示,以A为原点,AB,AD,AP所在的直线为坐标轴,建立空间直角坐标系,则C,D的坐标分别为C(a,a,0),D(0,2a,0),

因为PA⊥平面ABCD,∠PDA是PD与底面ABCD所成的角,
所以∠PDA=30°.
于是,在Rt△AED中,由AD=2a,得AE=a,
过E作EF⊥AD,垂足为F,在Rt△AFE中,
由AE=a,∠EAF=60°,得AF=![]() a,EF=
a,EF=![]() a.
a.
所以E(0,![]() a,
a,![]() a).
a).
于是,![]() =(0,
=(0,![]() a,
a,![]() a),
a),![]() =(-a,a,0).
=(-a,a,0).
设![]() 与DS
与DS![]() 的夹角为θ,则由
的夹角为θ,则由
cosθ=
=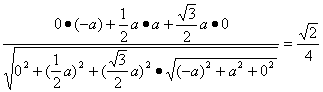 .
.
所以θ=arccos![]() .
.
所以AE与CD所成角的大小为arccos![]() .
.
点拨:求异面直线所成的角时,要注意它的范围是(0,![]() ].
].


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2012-2013学年湖南省株洲市高三第五次月考文科数学试卷(解析版) 题型:选择题
四棱锥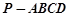 的三视图如右图所示,其中
的三视图如右图所示,其中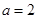 ,四棱锥
,四棱锥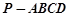 的五个顶点都在一个球面上,则该球表面积为( )
的五个顶点都在一个球面上,则该球表面积为( )
A.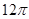 B.
B.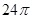 C.
C.
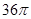 D.
D.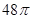
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
四棱锥 的三视图如右图所示,四棱锥
的三视图如右图所示,四棱锥 的五个顶点都在一个球面上,
的五个顶点都在一个球面上, 、
、 分别是棱
分别是棱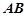 、
、 的中点,直线
的中点,直线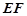 被球面所截得的线段长为
被球面所截得的线段长为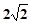 ,则该球表面积为 .
,则该球表面积为 .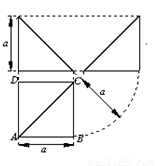
查看答案和解析>>
科目:高中数学 来源:2011-2012学年海南省高三高考极限压轴卷理科数学试卷(解析版) 题型:填空题
四棱锥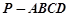 的三视图如右图所示,四棱锥
的三视图如右图所示,四棱锥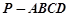 的五个顶点都在一个球面上,
的五个顶点都在一个球面上,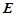 、
、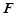 分别是棱
分别是棱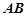 、
、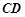 的中点,直线
的中点,直线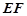 被球面所截得的线段长为
被球面所截得的线段长为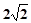 ,则该球表面积为 .
,则该球表面积为 .
查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间图形的基本关系与公理、空间图形的平行关系专项训练(河北) 题型:解答题
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.
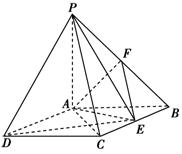 (1)求三棱锥E—PAD的体积;
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间图形的平行关系、垂直关系专项训练(河北) 题型:解答题
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com