
【题目】若有穷数列![]() (
(![]() 是正整数),满足
是正整数),满足![]() 即
即![]() (
(![]() 是正整数,且
是正整数,且![]() ),就称该数列为“对称数列”。例如,数列
),就称该数列为“对称数列”。例如,数列![]() 与数列
与数列![]() 都是“对称数列”.
都是“对称数列”.
(1)已知数列![]() 是项数为9的对称数列,且
是项数为9的对称数列,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列, ![]() ,
, ![]() ,试求
,试求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并求前9项和
,并求前9项和![]() .
.
(2)若![]() 是项数为
是项数为![]() 的对称数列,且
的对称数列,且![]() 构成首项为31,公差为
构成首项为31,公差为![]() 的等差数列,数列
的等差数列,数列![]() 前
前![]() 项和为
项和为![]() ,则当
,则当![]() 为何值时,
为何值时, ![]() 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求![]() 前
前![]() 项的和
项的和![]()
![]() .
.
科目:高中数学 来源: 题型:
【题目】甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2,3,4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球(左右手依次各取两球为两次取球)的成功取法次数为随机变量X,求X的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1.
(2)直线A1F∥平面ADE.
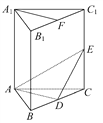
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届河北省衡水中学高三上学期六调】已知函数![]() ,其中
,其中![]() 均为实数,
均为实数,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,若对任意的
,若对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4 μg时治疗疾病有效,假若某病人一天中第一次服药为上午7:00,问:一天中怎样安排服药时间(共4次)效果最佳?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左焦点F为圆
的左焦点F为圆![]() 的圆心,且椭圆C上的点到点F的距离最小值为
的圆心,且椭圆C上的点到点F的距离最小值为![]() 。
。
(I)求椭圆C的方程;
(II)已知经过点F的动直线![]() 与椭圆C交于不同的两点A、B,点M坐标为(
与椭圆C交于不同的两点A、B,点M坐标为(![]() ),证明:
),证明: ![]() 为定值。
为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-3x+2≤0},集合B={y|y=x2-2x+a},集合C={x|x2-ax-4≤0}.命题p:A∩B≠;命题q:AC.
(1)若命题p为假命题,求实数a的取值范围;
(2)若命题p∧q为真命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com