
【题目】在直角坐标系![]() 中,动点
中,动点![]() (其中
(其中![]() )到点
)到点![]() 的距离的
的距离的![]() 倍与点
倍与点![]() 到直线
到直线![]() 的距离的
的距离的![]() 倍之和记为
倍之和记为![]() ,且
,且![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (
(![]() );(Ⅱ)
);(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据题意列出方程![]() ,化简即可求得;
,化简即可求得;
(Ⅱ)分析可知,曲线只包括部分图像,分两种具体情况讨论:当斜率不存在时和斜率存在时,先确定弦长![]() 对应斜率
对应斜率![]() 的范围,联立直线与椭圆的方程结合韦达定理表示出根与系数关系,利用焦半径公式表示出
的范围,联立直线与椭圆的方程结合韦达定理表示出根与系数关系,利用焦半径公式表示出![]() ,
,![]() ,结合前式韦达定理表示出关于
,结合前式韦达定理表示出关于![]() 的表达式,利用不等式性质即可求解
的表达式,利用不等式性质即可求解
(Ⅰ)依题意,![]()
![]() ,
,
![]()
化简得![]() ,
,
![]() 点
点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() (
(![]() ).
).
(Ⅱ)将![]() 代入曲线方程,解得
代入曲线方程,解得![]() ,设点
,设点![]() ,
,![]() .
.
由(Ⅰ)知,轨迹![]() 是椭圆
是椭圆![]() 在直线
在直线![]() 的右侧的部分(包括点
的右侧的部分(包括点![]() ).
).
可求出直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)当直线![]() 的斜率不存在时,设
的斜率不存在时,设![]() ,
,![]() ,
,
此时,![]() .
.
(2)当直线![]() 的斜率
的斜率![]() 存在时,直线
存在时,直线![]() 的方程为
的方程为![]() .
.
由已知,直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,
两点,
则![]() 或
或![]() .
.
设![]() ,
,![]() ,
,
由(Ⅰ)知,![]() ,
,![]() ,
,
所以![]()
![]()
由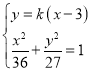 ,得
,得![]() .
.
则![]() ,
,
所以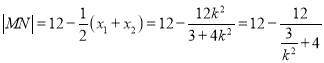
因为![]() 或
或![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以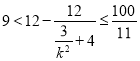 ,即
,即![]() .
.
综上可知,![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
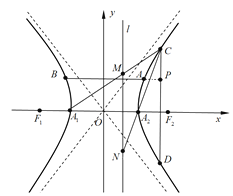
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在常数M,使得对任意
,若存在常数M,使得对任意![]() ,
,![]() 与
与![]() 中至少有一个不小于M,则记作
中至少有一个不小于M,则记作![]() ,那么下列命题正确的是( ).
,那么下列命题正确的是( ).
A.若![]() ,则数列
,则数列![]() 各项均大于或等于M;
各项均大于或等于M;
B.若![]() ,则
,则![]() ;
;
C.若![]() ,
,![]() ,则
,则![]() ;
;
D.若![]() ,则
,则![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,青蒿素作为一线抗疟药品得到大力推广某农科所为了深入研究海拔因素对青蒿素产量的影响,在山上和山下的试验田中分别种植了![]() 株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了
株青蒿进行对比试验.现在从山上和山下的试验田中各随机选取了![]() 株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
株青蒿作为样本,每株提取的青蒿素产量(单位:克)如下表所示:
编号位置 | ① | ② | ③ | ④ |
山上 |
|
|
|
|
山下 |
|
|
|
|
(1)根据样本数据,试估计山下试验田青蒿素的总产量;
(2)记山上与山下两块试验田单株青蒿素产量的方差分别为![]() ,
,![]() ,根据样本数据,试估计
,根据样本数据,试估计![]() 与
与![]() 的大小关系(只需写出结论);
的大小关系(只需写出结论);
(3)从样本中的山上与山下青蒿中各随机选取![]() 株,记这
株,记这![]() 株的产量总和为
株的产量总和为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“可构造三角形函数”.以下说法正确的是( )
A.f(x)=1(x∈R)不是“可构造三角形函数”
B.“可构造三角形函数”一定是单调函数
C.f(x)=![]() 是“可构造三角形函数”
是“可构造三角形函数”
D.若定义在R上的函数f(x)的值域是![]() (e为自然对数的底数),则f(x)一定是“可构造三角形函数”
(e为自然对数的底数),则f(x)一定是“可构造三角形函数”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆
的焦点重合,且此抛物线的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,试问直线
的垂直平分线,试问直线![]() 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com