
分析 (1)根据?q是?p的必要不充分条件,建立关于m的不等式并解之,即可得到实数m的取值范围;
(2)由关于x的不等式x2+2ax+4>0对一切x∈R恒成立可得△=4a2-16<0可得P;由函数f(x)=(3-2a)x是增函数可得3-2a>1可得q,若命题“p且q”为假命题,“p或q”为真命题,则p,q中一个为真,一个为假,分情况求解a.
解答 解:(1)∵p:{x|-2≤x≤10},
q:{x|1-m≤x≤1+m,m>0}.
∵?q是?p的必要不充分条件,
∴p是q的必要不充分条件,
∴$\left\{\begin{array}{l}{1-m≥-2}\\{1+m≤10}\end{array}\right.$,
(两个等号不同时成立)
解之得:m≤3,即实数m的取值范围是[3,+∞);
(2)由关于x的不等式x2+2ax+4>0对一切x∈R恒成立,
可得△=4a2-16<0,
∴P:-2<a<2,
由函数f(x)=(3-2a)x是增函数可得3-2a>1,
则a<1
q:a<1.
若命题“p且q”为假命题,“p或q”为真命题,则p,q中一个为真,一个为假
①若p真q假,则$\left\{\begin{array}{l}{-2<a<2}\\{a≥1}\end{array}\right.$,解得:1≤a<2,
②若P假q真,则$\left\{\begin{array}{l}{a≥2或a≤-2}\\{a<1}\end{array}\right.$,⇒a≤-2,
故答案为:(-∞,-2]∪[1,2).
点评 本题主要考查了p或q复合命题的真假的应用,解题的关键是利用二次函数的性质及指数函数的单调性准确求出命题p,q为真时a的范围.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
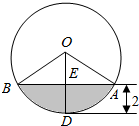 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )| A. | 4-$\frac{3\sqrt{3}}{4π}$ | B. | 2-$\frac{3\sqrt{3}}{16π}$ | C. | 3-$\frac{9\sqrt{3}}{4π}$ | D. | 3-$\frac{9\sqrt{3}}{16π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 432 | B. | 540 | C. | 1377 | D. | 1620 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com