
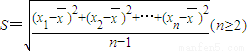 可作为总体标准差的点估计值;
可作为总体标准差的点估计值;

科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 1 |
| lgx |
| PA |
| PB |
| PC |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:高中数学综合题 题型:022
给出下列4个命题:
①直线![]() 到
到![]() 的角是
的角是![]() ;
;
②把直线![]() 绕原点按逆时针方向旋转,使它与圆x2+y2+
绕原点按逆时针方向旋转,使它与圆x2+y2+![]() -2y+3=0相切,
-2y+3=0相切,
则直线旋转的最小正角是![]() ;
;
③曲线y=4x-x2上取两点A(4,0),B(2,4),若曲线上一点P处的切线恰好平行于弦AB,则点P的坐标为(3,3);
④已知双曲线mx2-2my2=4的一条准线方程为y=4,则其渐近线方程为![]() .
.
其中错误的命题有______________.(把你认为错误命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com