
【题目】已知圆C:x2+y2=12,直线l:4x+3y=25.求圆C上任意一点A到直线l的距离小于2的概率.
【答案】解:设直线l':4x+3y﹣C=0,
l'与直线l:4x+3y=25的距离等于2,且与已知圆相交,
得 ![]() =2,解之得C=15或35
=2,解之得C=15或35
∵C<25,可得C=15
∴到直线l:4x+3y=25的距离等于2且与已知圆相交的直线
为直线l':4x+3y﹣15=0,
设l'交圆x2+y2=12于E、B两点,过圆心作EB的垂线,垂足为D,
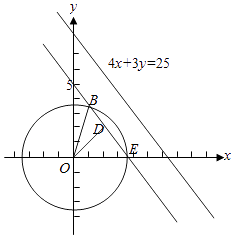
则D为EB的中点,
∵|OD|= ![]() =3,
=3,
∴Rt△EOD中,cos∠EOD= ![]() =
= ![]() ,得∠EOD=30°
,得∠EOD=30°
由此可得∠EOB=60°
当圆C上任意一点A到直线l的距离小于2时,点A位于劣弧BE上,
因此,所求概率为P= ![]() =
= ![]() .
.
【解析】根据平行线的距离公式,算出到直线l:4x+3y=25的距离等于2且与已知圆相交的直线为直线l':4x+3y﹣15=0.设l'交圆x2+y2=12于E、B两点,由图形观察可得当动点A位于劣弧BE上时点A到直线l的距离小于2.由此利用点到直线的距离公式,结合垂径定理和三角函数的定义算出∠EOB=60°,即可得到所求概率.
【考点精析】关于本题考查的几何概型,需要了解几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
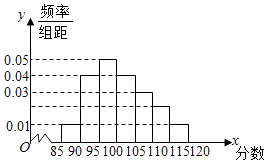
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100~110的学生数有21人. (Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占 ![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据(u1 , v1),(u2 , v2),,(un , vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为 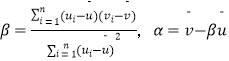 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C1:x2+y2=m与圆C2:x2+y2﹣6x﹣8y+16=0外切. (Ⅰ)求实数m的值;
(Ⅱ)若圆C1与x轴的正半轴交于点A,与y轴的正半轴交于点B,P为第三象限内一点,且点P在圆C1上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4). 
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得 ![]() +
+ ![]() =
= ![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图. 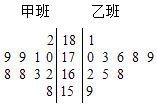
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sin(2x+
=(sin(2x+ ![]() ),sinx),
),sinx), ![]() =(1,sinx),f(x)=
=(1,sinx),f(x)= ![]() .
.
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,a=2 ![]() ,
, ![]() ,若
,若 ![]() sin(A+C)=2cosC,求b的大小.
sin(A+C)=2cosC,求b的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1中,如图E、F分别是BB1 , CD的中点, 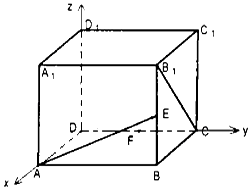
(1)求证:D1F⊥AE;
(2)求直线EF与CB1所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com