
分析 ①化简复数为a+bi的形式,求出复数z.
②直接利用复数的模求解即可.
③求出复数的对应点的坐标,即可得到结果.
④利用复数的基本概念求解即可.
⑤利用复数的幂运算求解即可.
解答 解:①复数z=$\frac{6-bi}{1+2i}$=$\frac{(6-bi)(1-2i)}{(1+2i)(1-2i)}$=$\frac{6-2b+(-12-b)i}{5}$,
复数z=$\frac{6-bi}{1+2i}$(其中i为虚数单位,b为实数)的实部和虚部互为相反数,
可得6-2b=12+b,解得b=-2,
z=2-2i.
②|2-2i|=$\sqrt{{2}^{2}+(-2)^{2}}$=2$\sqrt{2}$.
③复数z在复平面内对应的点(2,-2)在第四象限.
④z(m+i)=(2-2i)(m+i)=2m+2+(2-2m)i,是纯虚数,可得2m+2=0,解得m=-1.
⑤($\frac{z}{\overline{z}}$)2016=$(\frac{2+2i}{2-2i})^{2016}$=$[{(\frac{1+i}{1-i})^{2}]}^{1008}$=${[\frac{2i}{-2i}]}^{1008}$=1.
点评 本题考查复数的代数形式的混合运算,复数的模,复数的基本概念以及幂运算法则的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
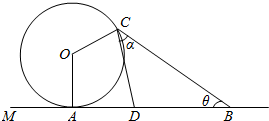 如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.
如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com