
(1)求点P的轨迹方程C;
(2)若曲线C为焦点在x轴上的椭圆,试求实数t的取值范围;
(3)若t=2,点M、N是C上关于原点对称的两个动点,点Q的坐标为(![]() ,3),求△QMN的面积S的最大值.
,3),求△QMN的面积S的最大值.
解:(1)设点A(a,0),B(0,b),P(x,y),∵![]() =t
=t![]() ,即(x-a,y)=t(-x,b-y),即
,即(x-a,y)=t(-x,b-y),即![]()
则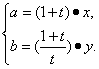 又∵|AB|=2,即a2+b2=4,∴
又∵|AB|=2,即a2+b2=4,∴![]() +
+![]() =1.
=1.
∴点P的轨迹方程C: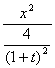 +
+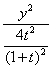 =1.
=1.
(2)∵曲线C为焦点在x轴上的椭圆,∴![]() >
>![]() ,得t2<1
,得t2<1![]() -1<t<1.
-1<t<1.
又∵t>0,∴0<t<1.
(3)当t=2时,曲线C的方程为![]() +
+![]() =1.
=1.
设M(x1,y1),N(-x1,-y1),则|MN|=2![]() .
.
当x1≠0时,设直线MN的方程为y=![]() x,则点Q到直线MN的距离h=
x,则点Q到直线MN的距离h=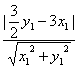 ,
,
∴△QMN的面积S=![]() ·2
·2![]() ·
·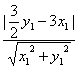 =|
=|![]() y1-3x1|.
y1-3x1|.
∴S2=|![]() y1-3x1|2=9x12+
y1-3x1|2=9x12+![]() y12-9x1y1.又∵
y12-9x1y1.又∵![]() +
+![]() =1,∴9x12+
=1,∴9x12+![]() y12=4.
y12=4.
∴S2=4-9x1y1.而1=![]() +
+![]() ≥-2·
≥-2·![]() ·
·![]() =
=![]() ,
,
则-9x1y1≤4,即S2≤8,S≤2![]() .当且仅当
.当且仅当![]() =
=![]() ,即x1=
,即x1=![]() y1时,“=”成立.
y1时,“=”成立.
当x1=0时,|MN|=![]() ,△QMN的面积S=
,△QMN的面积S=![]() ×
×![]() ×
×![]() =2.∴S的最大值是2
=2.∴S的最大值是2![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
| AP |
| PB |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
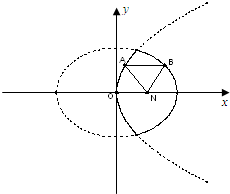 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
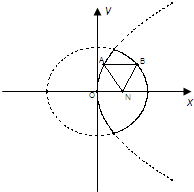 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012年福建省四地六校高二第二次月考理科数学 题型:选择题
已知动点A、B分别在图中抛物线 及椭圆
及椭圆
 的实线上运动,若
的实线上运动,若 ∥
∥ 轴,点N的坐标
轴,点N的坐标
为(1,0),则三角形ABN的周长 的取值范围是 ( )
的取值范围是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com