
定义向量的运算
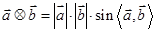 (其中
(其中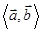 为向量
为向量 的夹角),设
的夹角),设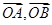 为非零向量,则下列说法正确的是 .
为非零向量,则下列说法正确的是 .
①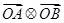 是非负实数
是非负实数
②若向量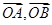 共线, 则有
共线, 则有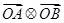 =0
=0
③若向量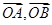 垂直,则有
垂直,则有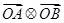 =0
=0
④若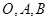 能构成三角形,则三角形面积
能构成三角形,则三角形面积
科目:高中数学 来源: 题型:
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| 1 |
| 2 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三第一学期期中考试试题数学 题型:解答题
(本题满分16分,第(1)小题6分,第(2)小题10分)
设 ,
, 定义一种向量的运算:
定义一种向量的运算: ,点P(x,y)在函数
,点P(x,y)在函数 的图像上运动,点Q在
的图像上运动,点Q在 的图像上运动,且满足
的图像上运动,且满足 (其中O为坐标原点)
(其中O为坐标原点)
(1)求函数f(x)的解析式;
(2)若函数 值域为
值域为 ,求a,b的值。
,求a,b的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() ,
,![]() 定义一种向量的运算:
定义一种向量的运算:![]() ,点P(x,y)在函数
,点P(x,y)在函数![]() 的图像上运动,点Q在
的图像上运动,点Q在![]() 的图像上运动,且满足
的图像上运动,且满足![]() (其中O为坐标原点)
(其中O为坐标原点)
(1)求函数f(x)的解析式;
(2)若函数![]() 值域为
值域为![]() ,求a,b的值。
,求a,b的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com