分析:(Ⅰ)由ABC-A1B1C1是正三棱柱,知AA1⊥平面ABC,BE⊥AA1.由△ABC是正三角形,E是AC中点,知BE⊥平面ACC1A1.由此能够证明平面BEC1⊥平面ACC1A1.
(Ⅱ)连B1C,设BC1∩B1C=D.由ABC-A1B1C1是正三棱柱,知BCC1B1是矩形,D是B1C的中点.由E是AC的中点,知AB1∥DE.由此能够证明AB1∥平面BEC1.
(Ⅲ)作CF⊥BC1于F,FG⊥BC1于G;连CG.由平面BEC1⊥平面ACC1A,知CF⊥平面BEC1,故FG是CG在平面BEC1上的射影.根据三垂线定理,知∠CGF是二面角E-BC1-C的平面角,由此能求出二面角E-BC1-C的大小.
解答:(Ⅰ)证明:∵ABC-A
1B
1C
1是正三棱柱,
∴AA
1⊥平面ABC,
∴BE⊥AA
1.
∵△ABC是正三角形,E是AC中点,
∴BE⊥AC,
∴BE⊥平面ACC
1A
1.
∴BE?平面BEC
1∴平面BEC
1⊥平面ACC
1A
1.…(4分)
(Ⅱ)证明:连B
1C,设BC
1∩B
1C=D.
∵ABC-A
1B
1C
1是正三棱柱,
∴BCC
1B
1是矩形,D是B
1C的中点.
∵E是AC的中点,
∴AB
1∥DE.
∵DE?平面BEC
1,AB
1?平面BEC
1,
∴AB
1∥平面BEC
1.…(8分)
(Ⅲ)解:作CF⊥BC
1于F,FG⊥BC
1于G;连CG.
∵平面BEC
1⊥平面ACC
1A,
∴CF⊥平面BEC
1…(9分)
∴FG是CG在平面BEC
1上的射影.
根据三垂线定理得,CG⊥BC
1.
∴∠CGF是二面角E-BC
1-C的平面角.…(10分)
设AB=a,∵
=,则A1A=a.
在Rt△ECC
1中,CF=
=a在Rt△BCC
1中,CG=
=a.
在Rt△CFG中,∵
sin∠CGF==,
∴∠CGF=45°.
∴二面角E-BC
1-C的大小是45°…(12分)
点评:本题考查证明平面BEC1⊥平面ACC1A1,求证AB1∥平面BEC1,求二面角E-BC1-C的大小.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点,易错点是∠CGF是二面角E-BC1-C的平面角的证明.解题时要认真审题,仔细解答.

 如图,正三棱柱ABC-A1B1C1中,E是AC中点.
如图,正三棱柱ABC-A1B1C1中,E是AC中点.

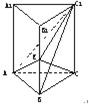 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.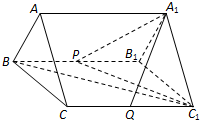 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.