
甲、乙两人进行围棋比赛,规定每局胜者得1分,负者得0分,比赛进行到有一方比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
(Ⅰ) ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)根据题意将第二局比赛结束时比赛停止的两种情况分析得到,然后利用互斥事件的概率公式求解; (Ⅱ)依题意知X的所有可能取值,然后利用独立事件的概率公式求解概率.
试题解析:(Ⅰ)当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛停止,故 , 3分
, 3分
解得 或
或 .又
.又 ,所以
,所以 . 5分
. 5分
(Ⅱ)依题意知X的所有可能取值为2,4,6。 6分
设每两局比赛为一轮,则该轮结束时比赛停止的概率为 ,若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响,从而有
,若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响,从而有
 ,
,
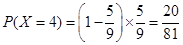 ,
,
 , 9分
, 9分
则随机变量的分布列为
|
X |
2 |
4 |
6 |
|
P |
|
|
|
故 . 12分
. 12分
考点:1.互斥和独立事件的概率;2.分布列和期望.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 9 |
查看答案和解析>>
科目:高中数学 来源:0127 模拟题 题型:解答题
 ),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为 。
。查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都外国语学校高三(上)10月月考数学试卷(解析版) 题型:解答题
 ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省师大附中等重点学校高三联考数学试卷(理科)(解析版) 题型:解答题
 ),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
),且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com