
分析 (1)由f(3)=5得出aln3=-5,再求出f($\frac{1}{3}$)的值.
(2)alnx≥-x2.然后讨论lnx的符号分离参数,转化为求-$\frac{{x}^{2}}{lnx}$得最大值或最小值问题.
解答 解:(1)∵f(3)=10+aln3=5,∴aln3=-5.∴f($\frac{1}{3}$)=$\frac{10}{9}$+aln$\frac{1}{3}$=$\frac{10}{9}$-aln3=$\frac{10}{9}+5$=$\frac{55}{9}$.
(2)∵x2+alnx+1≥1,∴alnx≥-x2.
①若lnx=0,即x=1时,显然上式恒成立.
②若lnx>0,即x>1时,a≥-$\frac{{x}^{2}}{lnx}$.令g(x)=-$\frac{{x}^{2}}{lnx}$.则g′(x)=$\frac{x(1-2lnx)}{l{n}^{2}x}$,
∴当1<x$<\sqrt{e}$时,g′(x)>0,当x$>\sqrt{e}$时,g′(x)<0,
∴当x=$\sqrt{e}$时,g(x)取得最大值g($\sqrt{e}$)=-2e.∴a≥-2e.
③若lnx<0,即0<x<1时,a≤-$\frac{{x}^{2}}{lnx}$,由②讨论可知g(x)在(0,1)上是增函数,且g(x)>0,∴a≤0.
综上,a的取值范围是[-2e,0].
点评 本题考查了函数求值及函数恒成立问题,分离参数法是常用解题方法之一.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
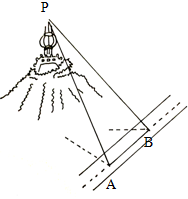 沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中
沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com