
【题目】已知f(x)=ax﹣lnx,x∈(0,e],g(x)= ![]() ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.
(1)讨论a=1时,函数f(x)的单调性和极值;
(2)求证:在(1)的条件下,f(x)>g(x)+ ![]() ;
;
(3)是否存在实数a使f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由.
【答案】
(1)
解:因为 ![]() ,所以当0<x<1时,f'(x)<0,此时函数f(x)单调递减.
,所以当0<x<1时,f'(x)<0,此时函数f(x)单调递减.
当1<x≤e时,f'(x)>0,此时函数f(x)单调递增.所以函数f(x)的极小值为f(1)=1.
(2)
证明:因为函数f(x)的极小值为1,即函数f(x)在(0,e]上的最小值为1.
又 ![]() ,所以当0<x<e时,g'(x)>0,此时g(x)单调递增.
,所以当0<x<e时,g'(x)>0,此时g(x)单调递增.
所以g(x)的最大值为g(e)= ![]() ,所以
,所以 ![]() ,所以在(1)的条件下,f(x)>g(x)+
,所以在(1)的条件下,f(x)>g(x)+ ![]() .
.
(3)
解:假设存在实数a,使f(x)=ax﹣lnx,x∈(0,e],有最小值3,则 ![]() ,
,
①当a≤0时,f'(x)<0,f(x)在(0,e]上单调递减, ![]() ,(舍去),此时函数f(x)的最小值不是3.
,(舍去),此时函数f(x)的最小值不是3.
②当0 ![]() 时,f(x)在(0,
时,f(x)在(0, ![]() ]上单调递减,f(x)在(
]上单调递减,f(x)在( ![]() ,e]上单调递增.
,e]上单调递增.
所以 ![]() ,满足条件.
,满足条件.
③当 ![]() 时,f(x)在(0,e]上单调递减,
时,f(x)在(0,e]上单调递减, ![]() ,(舍去),此时函数f(x)的最小值是不是3.
,(舍去),此时函数f(x)的最小值是不是3.
综上可知存在实数a=e2,使f(x)的最小值是3
【解析】(1)当a=1时,求函数的定义域,然后利用导数求函数的极值和单调性.(2)利用(1)的结论,求函数f(x)的最小值以及g(x)的最大值,利用它们之间的关系证明不等式.(3)利用导数求函数的最小值,让最小值等于3,解参数a.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的极值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】对于定义域为I的函数y=f(x),如果存在区间[m,n]I,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n],f(x)值域也是[m,n],则称[m,n]是函数y=f(x)的“好区间”.
(1)设g(x)=loga(ax﹣2a)+loga(ax﹣3a)(其中a>0且a≠1),求g(x)的定义域并判断其单调性;
(2)试判断(1)中的g(x)是否存在“好区间”,并说明理由;
(3)已知函数P(x)= ![]() (t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
(t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
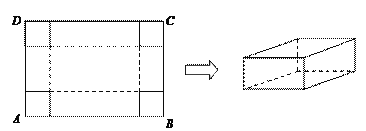
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于R上的可导函数f(x),若a>b>1且有(x﹣1)f′(x)≥0,则必有( )
A.f(a)+f(b)<2f(1)
B.f(a)+f(b)≤2f(1)
C.f(a)+f(b)≥2f(1)
D.f(a)+f(b)>2f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+(1﹣a) x2﹣a(a+2)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是﹣3,求a,b的值;
(2)若函数f(x)在区间(﹣1,1)上不单调,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:设![]() 为
为![]() 上的可导函数,若
上的可导函数,若![]() 为增函数,则称
为增函数,则称![]() 为
为![]() 上的凸函数.
上的凸函数.
(1)判断函数![]() 与
与![]() 是否为凸函数;
是否为凸函数;
(2)设![]() 为
为![]() 上的凸函数,求证:若
上的凸函数,求证:若![]() ,
, ![]() ,则
,则![]() 恒有
恒有![]() 成立;
成立;
(3)设![]() ,
, ![]() ,
, ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游景区的景点A处和B处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从A处出发,以50m/min的速度匀速步行,30min后到达B处,在B处停留20min后,再乘坐缆车回到A处.假设缆车匀速直线运动的速度为150m/mm.
(1)求该游客离景点A的距离y(m)关于出发后的时间x(mm)的函数解析式,并指出该函数的定义域;
(2)做出(1)中函数的图象,并求该游客离景点A的距离不小于1000m的总时长. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市2016年11月1日![]() 11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
| 2 |
|
| 1 |
|
| 4 |
|
| 6 |
|
| 10 |
|
| ||
| 2 |
|
(Ⅰ)完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污染指数在0![]() 50之间时,空气质量为优;在51
50之间时,空气质量为优;在51![]() 100之间时为良;在101
100之间时为良;在101![]() 150之间时,为轻微污染;在151
150之间时,为轻微污染;在151![]() 200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com