
【题目】(Ⅰ)设x≥1,y≥1,证明x+y![]() xy;
xy;
(Ⅱ)1≤a≤b≤c,证明logab+logbc+logca≤logba+logcb+logac.
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】
(Ⅰ)根据题意,首先对原不等式进行变形有x+y![]() xyxy(x+y)+1≤x+y+(xy)2;再用做差法,让右式﹣左式,通过变形、整理化简可得右式﹣左式=(xy﹣1)(x﹣1)(y﹣1),又由题意中x≥1,y≥1,判断可得右式﹣左式≥0,从而不等式得到证明.
xyxy(x+y)+1≤x+y+(xy)2;再用做差法,让右式﹣左式,通过变形、整理化简可得右式﹣左式=(xy﹣1)(x﹣1)(y﹣1),又由题意中x≥1,y≥1,判断可得右式﹣左式≥0,从而不等式得到证明.
(Ⅱ)首先换元,设logab=x,logbc=y,由换底公式可得:logba![]() ,logcb
,logcb![]() ,logac
,logac![]() ,logac=xy,将其代入要求证明的不等式可得:x+y
,logac=xy,将其代入要求证明的不等式可得:x+y![]() xy;又有logab=x≥1,logbc=y≥1,借助(Ⅰ)的结论,可得证明.
xy;又有logab=x≥1,logbc=y≥1,借助(Ⅰ)的结论,可得证明.
证明:(Ⅰ)由于x≥1,y≥1;则x+y![]() xyxy(x+y)+1≤x+y+(xy)2;
xyxy(x+y)+1≤x+y+(xy)2;
用作差法,右式﹣左式=(x+y+(xy)2)﹣(xy(x+y)+1)
=((xy)2﹣1)﹣(xy(x+y)﹣(x+y))
=(xy+1)(xy﹣1)﹣(x+y)(xy﹣1)
=(xy﹣1)(xy﹣x﹣y+1)
=(xy﹣1)(x﹣1)(y﹣1);
又由x≥1,y≥1,则xy≥1;即右式﹣左式≥0,从而不等式得到证明.
(Ⅱ)设logab=x,logbc=y,
由换底公式可得:logba![]() ,logcb
,logcb![]() ,logca
,logca![]() ,logac=xy,
,logac=xy,
于是要证明的不等式可转化为x+y![]() xy;
xy;
其中logab=x≥1,logbc=y≥1,
由(Ⅰ)的结论可得,要证明的不等式成立.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,关于函数
,关于函数![]() 有下列结论:
有下列结论:
①![]() ,
,![]() ;
;
②函数![]() 的图象是中心对称图形,且对称中心是
的图象是中心对称图形,且对称中心是![]() ;
;
③若![]() 是
是![]() 的极大值点,则
的极大值点,则![]() 在区间
在区间![]() 单调递减;
单调递减;
④若![]() 是
是![]() 的极小值点,且
的极小值点,且![]() ,则
,则![]() 有且仅有一个零点.
有且仅有一个零点.
其中正确的结论有________(填写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数对序列![]() 、
、![]() 、
、![]() 、
、![]() ,记
,记![]() ,
,![]() ,其中
,其中![]() 表示
表示![]() 和
和![]() 两个数中最大的数.
两个数中最大的数.
(1)对于数对序列![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)记![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 四个数中最小值,对于由两个数对
四个数中最小值,对于由两个数对![]() 、
、![]() 组成的数对序列
组成的数对序列![]() 、
、![]() 和
和![]() 、
、![]() ,试分别对
,试分别对![]() 和
和![]() 的两种情况比较
的两种情况比较![]() 和
和![]() 的大小;
的大小;
(3)在由![]() 个数对
个数对![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 组成的所有数对序列中,写出一个数对序列
组成的所有数对序列中,写出一个数对序列![]() 使
使![]() 最小,并写出
最小,并写出![]() 的值.(只需写出结论)
的值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
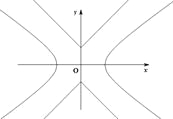
(1)在正确证明![]() 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆![]() 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD是菱形,![]() ,
,![]() 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
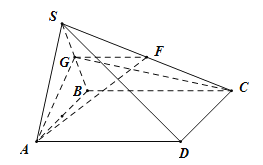
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD,![]() ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球运动被誉为“世界第一运动”.为推广足球运动,某学校成立了足球社团由于报名人数较多,需对报名者进行“点球测试”来决定是否录取,规则如下:
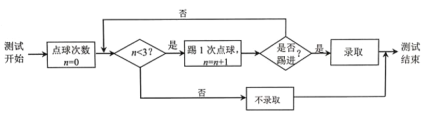
(1)下表是某同学6次的训练数据,以这150个点球中的进球频率代表其单次点球踢进的概率.为加入足球社团,该同学进行了“点球测试”,每次点球是否踢进相互独立,将他在测试中所踢的点球次数记为![]() ,求
,求![]() ;
;
![]()
(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,接到第n次传球的人即为第![]() 次触球者
次触球者![]() ,第n次触球者是甲的概率记为
,第n次触球者是甲的概率记为![]() .
.
(i)求![]() ,
,![]() ,
,![]() (直接写出结果即可);
(直接写出结果即可);
(ii)证明:数列![]() 为等比数列.
为等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com