
分析 由$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=0,可得渐近线方程;将内切圆的圆心坐标进行转化成圆与横轴切点Q的横坐标,PF1-PF2=F1Q-F2Q=6,F1Q+F2Q=F1F2解出OQ,即可求出△PF1F2的内切圆的圆心的横坐标.
解答 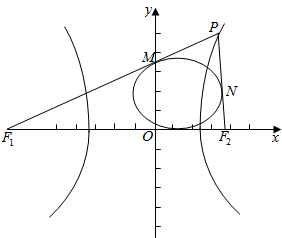 解:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1,其渐近线方程为y=±$\frac{2}{3}$x.
解:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1,其渐近线方程为y=±$\frac{2}{3}$x.
如图设切点分别为M,N,Q,则△PF1F2的内切圆的圆心的横坐标与Q横坐标相同.
由双曲线的定义,PF1-PF2=2a=6.
由圆的切线性质PF1-PF2=FIM-F2N=F1Q-F2Q=6,
∵F1Q+F2Q=F1F2=2$\sqrt{13}$,∴F2Q=3+$\sqrt{13}$,OQ=3,
∴Q横坐标为3.
故答案为:y=±$\frac{2}{3}$x;3.
点评 本题考查双曲线的方程与性质,考查双曲线的定义,巧妙地借助于圆的切线的性质是关键.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
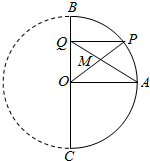 如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.
如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,4} | C. | {1} | D. | {2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com