
A.5π B.![]() π C.10π D.20π
π C.10π D.20π
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2011-2012学年安徽省蚌埠四校联盟高一自主招生考试数学试卷(解析版) 题型:填空题
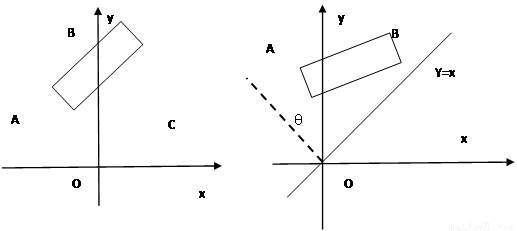
如图1,在平面直角坐标系中,边长为1的正方形OABC的顶点B在 轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
(1)当点A第一次落到 轴正半轴上时,求边BC在旋转过程中所扫过的面积;
轴正半轴上时,求边BC在旋转过程中所扫过的面积;
(2)若线段AB与 轴的交点为M(如图2),线段BC与直线
轴的交点为M(如图2),线段BC与直线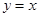 的交点为N.设
的交点为N.设 的周长为
的周长为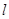 ,在正方形OABC旋转的过程中
,在正方形OABC旋转的过程中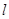 值是否有改变?并说明你的结论;
值是否有改变?并说明你的结论;
(3)设旋转角为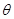 ,当
,当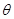 为何值时,
为何值时, 的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.
的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图a所示,正△ABC的边长为2![]() ,CD是AB边上的高,E、F分别是AC和BC边的中点.现将△ABC沿CD翻折成直二面角A―DC―B,如图b所示.
,CD是AB边上的高,E、F分别是AC和BC边的中点.现将△ABC沿CD翻折成直二面角A―DC―B,如图b所示.

(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角B―AC―D的大小;
(3)求点C到平面DEF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角B-AC-D的余弦值.
(文)如图,在三棱锥P—ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.
(1)证明AB⊥PC;
(2)证明PE∥平面FGH.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求异面直线AM与BC所成的角;
(2)求直线BA与平面ANC所成角的正弦值;
(3)在线段AB上,是否存在一个点Q,使MQ⊥平面ABC?若存在,试确定点Q的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com