
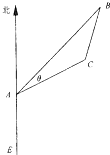
 如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距20
如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距20| 2 |
| 1 |
| 5 |
| 13 |
| 1 |
| 5 |
| 3 | ||
|
| 1 | ||
|
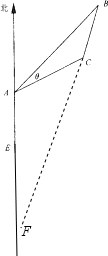 解:(1)由题意,AB=20
解:(1)由题意,AB=20| 2 |
| 13 |
| 1 |
| 5 |
| 5 | ||
|
| 5 |
5
| ||
|
| 5 |
| 800+125-325 | ||||
2×20
|
| 3 | ||
|
| 1 | ||
|
5
| ||
| sin(45°-B) |
| AF |
| sin(θ+B) |
| 1 |
| 5 |
| 1 | ||
|
| 5 | ||
|
5
| ||
| sin(45°-B) |


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
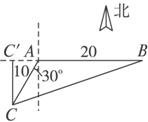
 如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距
如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距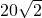 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中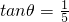 ,0°<θ<45°)且与观测站A相距
,0°<θ<45°)且与观测站A相距 海里的C处.
海里的C处.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
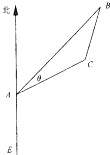
科目:高中数学 来源:2013年江苏省高考数学模拟试卷(一)(解析版) 题型:解答题
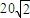 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中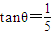 ,0°<θ<45°)且与观测站A相距
,0°<θ<45°)且与观测站A相距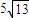 海里的C处.
海里的C处.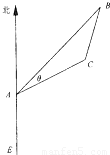
查看答案和解析>>
科目:高中数学 来源:2012年江苏省苏州大学高考数学考前指导试卷(解析版) 题型:解答题
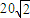 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中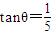 ,0°<θ<45°)且与观测站A相距
,0°<θ<45°)且与观测站A相距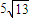 海里的C处.
海里的C处.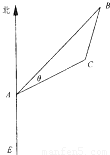
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com