
| A. | [-$\frac{5}{3}$,$\frac{5}{2}$] | B. | (-∞,-$\frac{5}{3}$]∪[$\frac{5}{2}$,+∞) | C. | (-∞,-$\frac{5}{2}$]∪[$\frac{5}{3}$,+∞) | D. | [-$\frac{5}{2}$,$\frac{5}{3}$] |
分析 直线ax+y+2=0过定点(0,-2),求出kMA=$\frac{3+2}{-2-0}$=-$\frac{5}{2}$,kMB=$\frac{3+2}{3-0}$=$\frac{5}{3}$,即可得出结论.
解答 解:直线ax+y+2=0恒过点M(0,-2),且斜率为-a,
∵kMA=$\frac{3+2}{-2-0}$=-$\frac{5}{2}$,kMB=$\frac{3+2}{3-0}$=$\frac{5}{3}$,
∵直线ax+y+2=0与线段AB有交点,
∴-a<-$\frac{5}{2}$或-a>$\frac{5}{3}$,
∴a∈(-∞,-$\frac{5}{3}$]∪[$\frac{5}{2}$,+∞),
故选:B.
点评 本题考点是两直线的交点坐标,考查直线与线段有公共点时参数的范围,本题直线ax+y+2=0形式简单,作答时易想不到这也是一个直线系方程,从而解不出定点致使题目无从下手.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$,36 | B. | $\frac{2}{3}$,18 | C. | $\frac{1}{6}$,72 | D. | $\frac{1}{2}$,24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
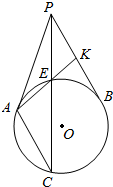 如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.
如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com