
【题目】(本小题满分14分)已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:当![]() 时,
时,![]() ;
;
(Ⅲ)确定实数![]() 的所有可能取值,使得存在
的所有可能取值,使得存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
科目:高中数学 来源: 题型:
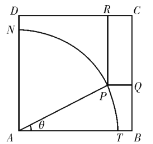
【题目】如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮![]() ,其中P是弧TN上一点.设
,其中P是弧TN上一点.设![]() ,长方形
,长方形![]() 的面积为S平方米.
的面积为S平方米.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
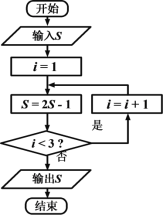
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 都是定义域为
都是定义域为![]() 的连续函数.已知:
的连续函数.已知:![]() 满足:①当
满足:①当![]() 时,
时,![]() 恒成立;②
恒成立;②![]() 都有
都有![]() .
.![]() 满足:①
满足:①![]() 都有
都有![]() ;②当
;②当![]() 时,
时,![]() .若关于
.若关于![]() 的不等式
的不等式![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )经过点
)经过点![]() ,且两个焦点
,且两个焦点![]() ,
,![]() 的坐标依次为
的坐标依次为![]() 和
和![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,证明:直线
,证明:直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
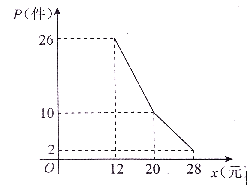
(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com