Question

【题目】设函数f（x）=x2﹣ax+a+3，g（x）=ax﹣2a．
（1）若函数h（x）=f（x）﹣g（x）在[﹣2，0]上有两个零点，求实数a的取值范围；
（2）若存在x0∈R，使得f（x0）≤0与g（x0）≤0同时成立，求实数a的最小值．

Answer 1

【答案】
（1）

解：由已知，h（x）=f（x）﹣g（x）=x2﹣2ax+3a+3=0在[﹣2，0]上有两个不同的实数解，

所以 ，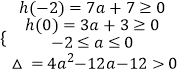

即 ，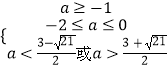

解得 ，

（2）

解：由已知， ，

（1）+（2）得 ，得a≥3，

再由（2）得x0≤2，由（1）得 ，得x0＞1，

于是，问题等价于：a≥3，且存在x0∈（1，2]满足 ，

令t=x0﹣1∈（0，1]， ，

因为 在（0，1]上单调递减，

所以φ（t）≥φ（1）=7，即a≥7，

故实数a的最小值为7．

【解析】（1）由h（x）在区间内的两个零点，结合图形，得到需要满足的条件．（2）由f（x0）≤0与g（x0）≤0同时成立，得到得a≥3，可将问题转化为最值问题，由单调性得到最值，即可．