
分析 (1)题意,利用对数换底公式log(c+b)a=loga(c+b),log(c-b)a=loga(c-b),证明左端=右端即可;
(2)由题意可得b1=a1λ,…,bn=anλ,从而证得结合.
解答 证明:(1)由勾股定理得a2+b2=c2,即a2=c2-b2,
∴右边=2log(c+b)a•log(c-b)a=$\frac{2}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{{log}_{a}{a}^{2}}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{{log}_{a}{(c}^{2}-{b}^{2})}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{{log}_{a}(c-b)+{log}_{a}(c+b)}{{log}_{a}(c+b){log}_{a}(c-b)}$=$\frac{1}{{log}_{a}(c+b)}$+$\frac{1}{{log}_{a}(c-b)}$=log(c+b)a+log(c-b)a=左边,
∴原等式成立;
(2)∵log${\;}_{{a}_{1}}$b1=log${\;}_{{a}_{2}}$b2=…=log${\;}_{{a}_{n}}$bn=λ,
∴b1=a1λ,…,bn=anλ,
∴b1b2…bn=a1λ•…•anλ=(a1a2a3…an)λ,
∴log${\;}_{{a}_{1}{a}_{2}…{a}_{n}}$(b1b2…bn)=λ.
点评 本题考查对数换底公与对数运算性质的应用,考查正向思维与逆向思维的综合应用,考查推理证明与运算能力,属于中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
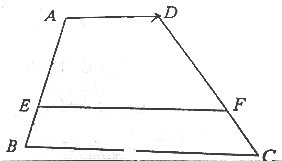 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com