
【题目】设![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,问:是否存在实数c使得
,问:是否存在实数c使得![]() 对所有
对所有![]() 成立?证明你的结论.
成立?证明你的结论.
【答案】(1)![]() (2)存在;证明见解析;
(2)存在;证明见解析;
【解析】
(1)根据已知条件证得数列![]() 是等差数列,由此求得
是等差数列,由此求得![]() ,进而求得数列
,进而求得数列![]() 的通项公式.
的通项公式.
(2)设![]() ,则
,则![]() .利用数学归纳法证得
.利用数学归纳法证得![]() 、
、![]() .进而证得
.进而证得![]() 、
、![]() ,从而证得结论成立.
,从而证得结论成立.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
两边平方得:![]() .
.
从而![]() 是首项为
是首项为![]() ,公差为1的等差数列,
,公差为1的等差数列,
故![]() ,
,
由于![]() ,即
,即![]() ,
,
所以![]()
(2)设![]() ,则
,则![]() .
.
先证:![]() .①
.①
当![]() 时,结论明显成立.
时,结论明显成立.
假设![]() 时结论成立,即
时结论成立,即![]() .
.
由于![]() 在
在![]() 上为减函数,从而
上为减函数,从而
![]() .
.
即![]() .这就是说,当
.这就是说,当![]() 时结论成立故①成立.
时结论成立故①成立.
再证:![]() .②
.②
当![]() 时,
时,![]() ,所以
,所以![]() ,即
,即![]() 时②成立.
时②成立.
假设![]() 时,结论成立,即
时,结论成立,即![]() .
.
由①及![]() 在
在![]() 上为减函数,得
上为减函数,得
![]() ,
,
![]() .
.
这就是说,当![]() 时②成立.所以②对一切
时②成立.所以②对一切![]() 成立.
成立.
由②得![]() ,
,
即![]() ,
,
因此![]() ③.
③.
又由①②及![]() 在
在![]() 上为减函数,得
上为减函数,得![]() ,即
,即![]() .
.
![]() .解得
.解得![]() ④.
④.
综上,由②③④知,存在![]() ,使
,使![]() 对一切
对一切![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】一辆汽车从起点![]() 出发开到终点
出发开到终点![]() (不允许反向行驶),
(不允许反向行驶),![]() 的距离为2007.在沿途设立了一些车站,所有到
的距离为2007.在沿途设立了一些车站,所有到![]() 的距离是100的倍数的地方都设立了车站(这些车站的集合设为
的距离是100的倍数的地方都设立了车站(这些车站的集合设为![]() ),所有到
),所有到![]() 的距离是223的倍数的地方也都设立了车站(这些车站的集合设为
的距离是223的倍数的地方也都设立了车站(这些车站的集合设为![]() ).该车在行驶途中的每次停车,要么在距其最近的集合
).该车在行驶途中的每次停车,要么在距其最近的集合![]() 中的车站停车,要么在距其最近的集合
中的车站停车,要么在距其最近的集合![]() 中的车站停车.则由
中的车站停车.则由![]() 驶到
驶到![]() 的所有可能的停车方式的数目
的所有可能的停车方式的数目![]() 在区间( )中.
在区间( )中.
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,O为坐标原点,点![]() ,
,![]() ,Q为平面上的动点,且
,Q为平面上的动点,且![]() ,线段
,线段![]() 的中垂线与线段
的中垂线与线段![]() 交于点P.
交于点P.
![]() 求
求![]() 的值,并求动点P的轨迹E的方程;
的值,并求动点P的轨迹E的方程;
![]() 若直线l与曲线E相交于A,B两点,且存在点
若直线l与曲线E相交于A,B两点,且存在点![]() 其中A,B,D不共线
其中A,B,D不共线![]() ,使得
,使得![]() ,证明:直线l过定点.
,证明:直线l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() 是正整数,且
是正整数,且![]() ,…,则称
,…,则称![]() 为“绝对差数列”.
为“绝对差数列”.
(1)举出一个前5项不为零的“绝对差数列”(只要求写出前10项);
(2)若“绝对差数列”![]() 中,
中,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,…,分别判断当
,…,分别判断当![]() 时,
时,![]() 与
与![]() 的极限是否存在?如果存在,求出其极限值.
的极限是否存在?如果存在,求出其极限值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年9月支付宝宣布在肯德基的KPRO餐厅上线刷脸支付,也即用户可以不用手机,单单通过刷脸就可以完成支付宝支付,这也是刷脸支付在全球范围内的首次商用试点.某市随机抽查了每月用支付宝消费金额不超过3000元的男女顾客各300人,调查了他们的支付宝使用情况,得到如下频率分布直方图:
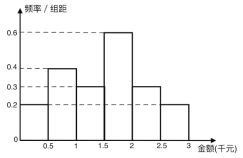
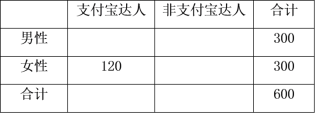
若每月利用支付宝支付金额超过2千元的顾客被称为“支付宝达人”, 利用支付宝支付金额不超过2千元的顾客称为“非支付宝达人”.
(I)若抽取的“支付宝达人”中女性占120人,请根据条件完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
(II)支付宝公司为了进一步了解这600人的支付宝使用体验情况和建议,从“非支付宝达人” “支付宝达人”中用分层抽样的方法抽取8人.若需从这8人中随机选取2人进行问卷调查,求至少有1人是“支付宝达人”的概率.
附:参考公式与参考数据如下
![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点O为坐标原点,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,离心率为
(a>b>0)的左、右焦点分别为F1,F2,离心率为![]() ,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为
,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为![]() .
.
(1)求椭圆C的标准方程;
(2)过点H(-2,0)的直线交椭圆C于A,B两点,若AF1⊥BF1,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
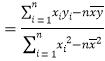 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com