练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】关于函数，有下述四个结论：

    ①若在内单调递增，则.

    ②若在内单调递减，则.

    ③若在内有且仅有一个极大值点，则.

    ④若在内有且仅有一个极小值点，则.

    其中所有正确结论的序号是（ ）

    A.①③B.②③C.①④D.③④

    【答案】A

    【解析】

    根据三角函数的单调性判断①②的正确性；根据三角函数的极值点判断③④的正确性.

    依题意函数，

    由，解得（），

    若在内单调递增，则.所以①正确.

    由，解得（），

    若在内单调递减，则，此不等式组无解.所以②错误.

    对于③，由，解得（），依题意在内有且仅有一个解，即且，

    即且，即且，所以的取值范围是，所以③正确.

    对于④，由，解得（），依题意在内有且仅有一个解，即且，

    即且，即且，所以的取值范围是，所以④错误.

    故正确的为①③.

    故选：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校为了增强学生的记忆力和辨识力，组织了一场类似《最强大脑》的PK赛，两队各由4名选手组成，每局两队各派一名选手PK，比赛四局.除第三局胜者得2分外，其余各局胜者均得1分，每局的负者得0分.假设每局比赛A队选手获胜的概率均为，且各局比赛结果相互独立，比赛结束时A队的得分高于B队的得分的概率为( )

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2017·石家庄一模)祖暅是南北朝时期的伟大数学家，5世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积一定相等．现有以下四个几何体：图①是从圆柱中挖去一个圆锥所得的几何体，图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为(　　)

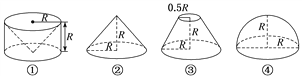
    A. ①② B. ①③

    C. ②④ D. ①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】疫情期间，一同学通过网络平台听网课，在家坚持学习.某天上午安排了四节网课，分别是数学，语文，政治，地理，下午安排了三节，分别是英语，历史，体育.现在，他准备在上午下午的课程中各任选一节进行打卡，则选中的两节课中至少有一节文综学科（政治、历史、地理）课程的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年3月5日上午，李克强总理做政府工作报告时表示，将新能源汽车车辆购置税优惠政策再延长三年，自2018年1月1日至2020年12月31日，对购置的新能源汽车免征车辆购置税.新能源汽车销售的春天来了！从衡阳地区某品牌新能源汽车销售公司了解到，为了帮助品牌迅速占领市场，他们采取了保证公司正常运营的前提下实行薄利多销的营销策略（即销售单价随日销量（台）变化而有所变化），该公司的日盈利（万元），经过一段时间的销售得到，的一组统计数据如下表：

    日销量台

    1

    2

    3

    4

    5

    日盈利万元

    6

    13

    17

    20

    22

    将上述数据制成散点图如图所示：

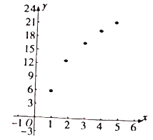
    （1）根据散点图判断与中，哪个模型更适合刻画，之间的关系？并从函数增长趋势方面给出简单的理由；

    （2）根据你的判断及下面的数据和公式，求出关于的回归方程，并预测当日销量时，日盈利是多少？

    参考公式及数据：线性回归方程，其中，；

    ，，

    ，.

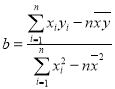    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年入冬时节，长春市民为了迎接2022年北京冬奥会，增强身体素质，积极开展冰上体育锻炼.现从速滑项目中随机选出100名参与者，并由专业的评估机构对他们的锻炼成果进行评估打分（满分为100分）并且认为评分不低于80分的参与者擅长冰上运动，得到如图所示的频率分布直方图：

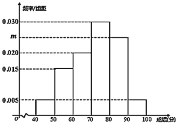
    （1）求的值；

    （2）将选取的100名参与者的性别与是否擅长冰上运动进行统计，请将下列列联表补充完整，并判断能否在犯错误的概率在不超过0.01的前提下认为擅长冰上运动与性别有关系？

    擅长

    不擅长

    合计

    男性

    30

    女性

    50

    合计

    100

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

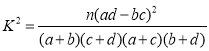    （，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对某两名高三学生在连续9次数学测试中的成绩（单位：分）进行统计得到折线图，下面是关于这两位同学的数学成绩分析．

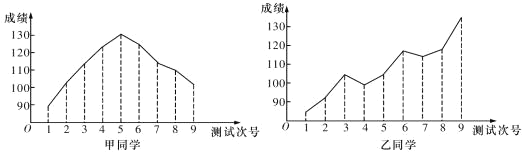
    ①甲同学的成绩折线图具有较好的对称性，故平均成绩为130分；

    ②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间内；

    ③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关；

    ④乙同学连续九次测验成绩每一次均有明显进步．

    其中正确的个数为（　　）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，其中．

    (1)若是函数的极值点，求实数的值；

    (2)若对任意的（为自然对数的底数）都有≥成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最，编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”，见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注，还得到了无数外国人的关注.某单位有10位外国人，其中关注此次大阅兵的有8位，若从这10位外国人中任意选取3位做一次采访，则被采访者中至少有2位关注此次大阅兵的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案