
已知函数
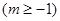 .
.
(Ⅰ)讨论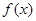 的单调性;
的单调性;
(Ⅱ)设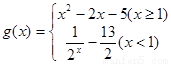 .当
.当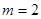 时,若对任意
时,若对任意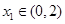 ,
,
存在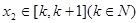 ,使
,使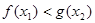 ,求实数
,求实数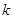 的最小值
的最小值
(Ⅰ) 当 时,函数
时,函数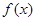 的单调递增区间为
的单调递增区间为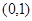 ,单调递减区间为
,单调递减区间为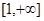 ;
;
当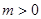 时,函数
时,函数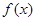 单调递增区间为
单调递增区间为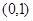 和
和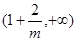 ,单调递减区间
,单调递减区间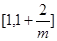
(Ⅱ)4
【解析】解:(Ⅰ)由题,函数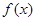 的定义域为
的定义域为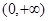
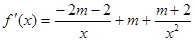

(1)若 ,则
,则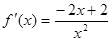 ,
,
从而当 时,
时,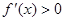 ;当
;当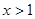 时,
时, ,
,
此时函数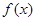 的单调递增区间为
的单调递增区间为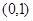 ,单调递减区间为
,单调递减区间为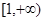 ;------------3分
;------------3分
(2)若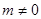 ,则
,则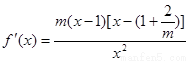 ,
,
①当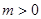 时,因为
时,因为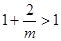 ,从而当
,从而当 或
或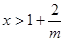 时,
时,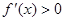 ;当
;当 时,
时, ,
,
此时函数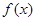 的单调递增区间为
的单调递增区间为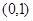 和
和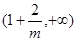 ,单调递减区间为
,单调递减区间为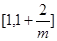 ;
;
②当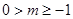 时,
时,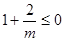 ,
,
函数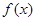 的单调递增区间为
的单调递增区间为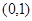 ,单调递减区间为
,单调递减区间为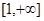 ;
;
综上所述,当 时,函数
时,函数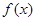 的单调递增区间为
的单调递增区间为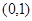 ,单调递减区间为
,单调递减区间为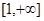 ;
;
当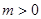 时,函数
时,函数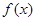 单调递增区间为
单调递增区间为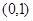 和
和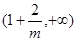 ,单调递减区间
,单调递减区间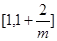 8分
8分
(Ⅱ)由(Ⅰ)可得当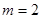 时,函数
时,函数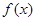 在区间
在区间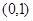 上单调递增,在
上单调递增,在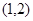 上单调递减,
上单调递减,
所以在区间 上,
上,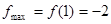 ,
,
由题,对任意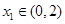 ,存在
,存在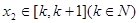 ,使
,使 ,
,
从而存在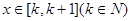 ,使
,使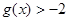 ,
,
即只需函数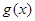 在区间
在区间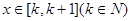 上的最小值大于
上的最小值大于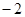 ,
,
又当 时,
时, 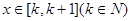 时,
时,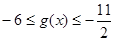 ,不符
,不符
所以在区间 上
上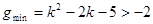 ,解得
,解得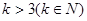 ,
,
所以实数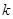 的最小值为4.
-------------15分
的最小值为4.
-------------15分


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com