
【题目】已知等比数列{an}中a2=2,a5= ![]() ,则a1a2+a2a3+a3a4+…+anan+1等于( )
,则a1a2+a2a3+a3a4+…+anan+1等于( )
A.16(1﹣4﹣n)
B.16(1﹣2n)
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
已知函数f(x)=(x2+bx+b)![]() (b∈R).
(b∈R).
(1)当b=4时,求f(x)的极值;
(2)若f(x)在区间![]() 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是
①任取x>0,均有3x>2x .
②当a>0,且a≠1时,有a3>a2 .
③y=( ![]() )﹣x是增函数.
)﹣x是增函数.
④y=2|x|的最小值为1.
⑤在同一坐标系中,y=2x与y=2﹣x的图象关于y轴对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C对应的边分别a,b,c,且acosC,bcosB,ccosA成等差数列,则角B等于( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(Ⅰ)求f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离. 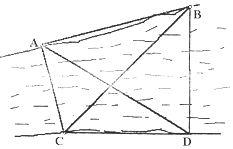
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取![]() 件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表
内,则为合格品,否则为不合格品.表![]() 是甲流水线样本的频数分布表,图
是甲流水线样本的频数分布表,图![]() 是乙流水线样本的频率分布直方图.
是乙流水线样本的频率分布直方图.
表 | ||||||||||||
|
图 |
|
(Ⅰ)根据图![]() ,估计乙流水线生产产品该质量指标值的中位数.
,估计乙流水线生产产品该质量指标值的中位数.
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了![]() 件产品,则甲,乙两条流水线分别生产出不合格品约多少件.
件产品,则甲,乙两条流水线分别生产出不合格品约多少件.
(Ⅲ)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:  (其中
(其中![]() 样本容量)
样本容量)
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com