练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列四个结论：

    ①在回归分析模型中，残差平方和越大，说明模型的拟合效果越好；

    ②某学校有男教师60名、女教师40名，为了解教师的体育爱好情况，在全体教师中抽取20名调查，则宜采用的抽样方法是分层抽样；

    ③线性相关系数越大，两个变量的线性相关性越弱；反之，线性相关性越强；

    ④在回归方程中，当解释变量每增加一个单位时，预报变量增加0.5个单位.

    其中正确的结论是（ ）

    A. ①②B. ①④

    C. ②③D. ②④

    【答案】D

    【解析】

    根据残差的意义可判断①；根据分成抽样特征，判断②；根据相关系数的意义即可判断③；由回归方程的系数，可判断④。

    根据残差的意义，可知当残差的平方和越小，模拟效果越好，所以①错误；

    当个体差异明显时，选用分层抽样法抽样，所以②正确；

    根据线性相关系数特征，当相关系数越大，两个变量的线性相关性越强，所以③错误；

    根据回归方程的系数为0.5，所以当解释变量每增加一个单位时，预报变量增加0.5个单位.

    综上，②④正确，故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知过点的动直线与圆相交于，两点，是中点，与直线相交于.

    (1)当与垂直时，求的方程；

    (2)当时，求直线的方程；

    (3)探究是否与直线的倾斜角有关？若无关，求出其值；若有关，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】连接正方体每个面的中心构成一个正八面体，则该八面体的外接球与内切球体积之比为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某化工企业2018年年底投入100万元，购入一套污水处理设备。该设备每年的运转费用是0.5万元，此外，每年都要花费一定的维护费，第一年的维护费为2万元，由于设备老化，以后每年的维护费都比上一年增加2万元。设该企业使用该设备年的年平均污水处理费用为（单位：万元）

    （1）用表示；

    （2）当该企业的年平均污水处理费用最低时，企业需重新更换新的污水处理设备。则该企业几年后需要重新更换新的污水处理设备。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，是边长为2的正三角形，是的中点，是的中点.

    （1）证明：平面；

    （2）若，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】工厂抽取了在一段时间内生产的一批产品，测量一项质量指标值，绘制了如图所示的频率分布直方图.

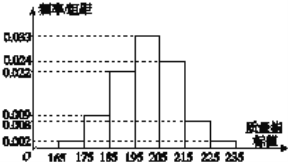
    （1）计算该样本的平均值，方差；（同一组中的数据用该组区间的中点值作代表）

    （2）若质量指标值在之内为一等品.

    （i）用样本估计总体，问该工厂一天生产的产品是否有以上为一等品？

    （ii）某天早上、下午分别抽检了50件产品，完成下面的表格，并根据已有数据，判断是否有的把握认为一等品率与生产时间有关？

    一等品个数

    非一等品个数

    总计

    早上

    36

    50

    下午

    26

    50

    总计

    附：.

    0.25

    0.15

    0.10

    0.050

    0.010

    0.001

    1.323

    2.072

    2.706

    3.841

    6.635

    10.828

    参考数据：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知线段AB的端点B的坐标是（4，2），端点A在圆C：（x+2）2+y2＝16上运动．

    （1）求线段AB的中点的轨迹方程H．

    （2）判断（1）中轨迹H与圆C的位置关系．

    （3）过点P（3，2）作两条相互垂直的直线MN，EF，分别交（1）中轨迹H于M，N和E，F，求四边形MNFE面积的最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）讨论函数的单调性

    （2）函数，且．若在区间（0，2）内有零点，求实数m的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知椭圆： 的长轴为，过点的直线与轴垂直，椭圆上一点与椭圆的长轴的两个端点构成的三角形的最大面积为2，且椭圆的离心率为.

    （1）求椭圆的标准方程；

    （2） 设是椭圆上异于， 的任意一点，连接并延长交直线于点， 点为的中点，试判断直线与椭圆的位置关系，并证明你的结论.

    查看答案和解析>>

    同步练习册答案