
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示的圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形的圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.

乙商场:从装有2个白球、2个蓝球和2个红球(这些球除颜色外完全相同)的盒子中一次性摸出2球,若摸到的是2个相同颜色的球,则为中奖.
试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
【答案】答案见解析
【解析】试题分析:根据概率公式分别计算,由几何概型概率公式求得P(A) ![]() . 由古典概型概率公式求得P(B)=
. 由古典概型概率公式求得P(B)= ![]() 比较即可.
比较即可.
试题解析:设顾客去甲商场转动圆盘,指针指向阴影部分为事件A,试验的全部结果构成的区域为圆盘,面积为πr2(r为圆盘的半径),阴影区域的面积为S=![]() ·π r2=
·π r2=![]() π r2.由几何概型概率公式,得P(A)=
π r2.由几何概型概率公式,得P(A)= 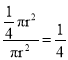 .
.
设顾客去乙商场一次摸出两个相同颜色的球为事件B,
记2个白球为白1,白2;2个红球为红1、红2;2个蓝球为蓝1、蓝2.
则从盒子中一次性摸出2球,一切可能的结果有:
(白1,白2),(白1,红1)、(白1,红2),(白1,蓝1),(白1,蓝2);
(白2,红1),(白2,红2),(白2,蓝1),(白2,蓝2);
(红1,红2),(红1,蓝1),(红1,蓝2);
(红2,蓝1),(红2,蓝2);
(蓝1,蓝2),共15种;
其中摸到的是2个相同颜色的球有(白1,白2),(红1,红2),(蓝1,蓝2),共3种;
由古典概型概率公式,得P(B)= ![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)证明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2017年8月18日某省x个监测点数据统计如下:
空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
监测点个数 | 15 | 40 | y | 10 |

(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)在空气污染指数分别为50~100和150~200的监测点中,用分层抽样的方法抽取5个监测点,从中任意选取2个监测点,事件A“两个都为良”发生的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出30个数:1,2,4,7,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),请在图中判断框内①处和执行框中的②处填上合适的语句,使之能完成该题算法功能.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数  下列四个命题: ①f(f(1))>f(3);
下列四个命题: ①f(f(1))>f(3);
②x0∈(1,+∞), ![]() ;
;
③f(x)的极大值点为x=1;
④x1 , x2∈(0,+∞),|f(x1)﹣f(x2)|≤1
其中正确的有 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点O为坐标原点,椭圆 ![]() 的右顶点为A,上顶点为B,过点O且斜率为
的右顶点为A,上顶点为B,过点O且斜率为 ![]() 的直线与直线AB相交M,且
的直线与直线AB相交M,且 ![]() .
.
(Ⅰ)求证:a=2b;
(Ⅱ)PQ是圆C:(x﹣2)2+(y﹣1)2=5的一条直径,若椭圆E经过P,Q两点,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球. (Ⅰ)求开始第4次发球时,甲、乙的比分为1比2的概率;
(Ⅱ)ξ表示开始第4次发球时乙的得分,求ξ的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com