
ЎҫМвДҝЎҝ№ъДЪДіЦӘГыБ¬Лшөк·ЦөкҝӘХЕУӘТөЖЪјдЈ¬ФЪ№М¶ЁөДКұјд¶ОДЪПы·СҙпөҪТ»¶ЁұкЧјөД№ЛҝНҝЙҪшРРТ»ҙОійҪұ»о¶ҜЈ¬ЛжЧЕійҪұ»о¶ҜөДУРР§ҝӘХ№Ј¬ІОУлійҪұ»о¶ҜөДИЛКэФҪАҙФҪ¶аЈ¬ёГ·ЦөкҫӯАн¶ФҝӘТөЗ°![]() МмІОјУійҪұ»о¶ҜөДИЛКэҪшРРНіјЖЈ¬
МмІОјУійҪұ»о¶ҜөДИЛКэҪшРРНіјЖЈ¬ ![]() ұнКҫҝӘТөөЪ
ұнКҫҝӘТөөЪ![]() МмІОјУійҪұ»о¶ҜөДИЛКэЈ¬өГөҪНіјЖұнёсИзПВЈә
МмІОјУійҪұ»о¶ҜөДИЛКэЈ¬өГөҪНіјЖұнёсИзПВЈә
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ҫӯ№эҪшТ»ІҪНіјЖ·ЦОцЈ¬·ўПЦ![]() Ул
Ул![]() ҫЯУРПЯРФПа№Ш№ШПө.
ҫЯУРПЯРФПа№Ш№ШПө.
ЈЁ1Ј©ёщҫЭЙПұнМṩөДКэҫЭЈ¬УГЧоРЎ¶юіЛ·ЁЗуіц![]() №ШУЪ
№ШУЪ![]() өДПЯРФ»Ш№й·ҪіМ
өДПЯРФ»Ш№й·ҪіМ![]() Ј»
Ј»
ЈЁ2Ј©ИфёГ·ЦөкҙЛҙОійҪұ»о¶ҜЧФҝӘТөКјЈ¬іЦРш![]() МмЈ¬ІОјУійҪұөДГҝО»№ЛҝНійөҪТ»өИҪұЈЁјЫЦө
МмЈ¬ІОјУійҪұөДГҝО»№ЛҝНійөҪТ»өИҪұЈЁјЫЦө![]() ФӘҪұЖ·Ј©өДёЕВКОӘ
ФӘҪұЖ·Ј©өДёЕВКОӘ![]() Ј¬ійөҪ¶юөИҪұЈЁјЫЦө
Ј¬ійөҪ¶юөИҪұЈЁјЫЦө![]() ФӘҪұЖ·Ј©өДёЕВКОӘ
ФӘҪұЖ·Ј©өДёЕВКОӘ![]() Ј¬ійөҪИэөИҪұЈЁјЫЦө
Ј¬ійөҪИэөИҪұЈЁјЫЦө![]() ФӘҪұЖ·Ј©өДёЕВКОӘ
ФӘҪұЖ·Ј©өДёЕВКОӘ![]() .
.
КФ№АјЖёГ·ЦөкФЪҙЛҙОійҪұ»о¶ҜҪбКшКұЛНіц¶аЙЩФӘҪұЖ·Јҝ
ІОҝј№«КҪЈә 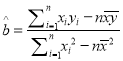 Ј¬
Ј¬ ![]() .
.
Ўҫҙр°ёЎҝЈЁ1Ј©![]() ЈЁ2Ј©
ЈЁ2Ј©![]()
ЎҫҪвОцЎҝКФМв·ЦОц:ЈЁ1Ј©УЙ№«КҪ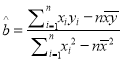 Ј¬ҝЙөГ
Ј¬ҝЙөГ![]() Ј¬ФЩЗуҫщЦө
Ј¬ФЩЗуҫщЦө![]() Ј¬ІўУЙ
Ј¬ІўУЙ![]() ҝЙөГ
ҝЙөГ![]() Ј¬Ҫш¶шҝЙөГПЯРФ»Ш№й·ҪіМ
Ј¬Ҫш¶шҝЙөГПЯРФ»Ш№й·ҪіМ![]() Ј»ЈЁ2Ј©ПИёщҫЭКэС§ЖЪНы№«КҪЗуГҝО»»сҪұҪұҪрөДЖЪНы
Ј»ЈЁ2Ј©ПИёщҫЭКэС§ЖЪНы№«КҪЗуГҝО»»сҪұҪұҪрөДЖЪНы![]() Ј¬ФЩёщҫЭПЯРФ»Ш№й·ҪіМФӨІвөЪ8,9,10МмИЛКэЈ¬өГөҪ10МмЧЬИЛКэЈ¬ЧоәуёщҫЭіЛ»эөГөҪЧЬҪұҪрКэ.
Ј¬ФЩёщҫЭПЯРФ»Ш№й·ҪіМФӨІвөЪ8,9,10МмИЛКэЈ¬өГөҪ10МмЧЬИЛКэЈ¬ЧоәуёщҫЭіЛ»эөГөҪЧЬҪұҪрКэ.
КФМвҪвОцЈәЈЁ1Ј©ТАМвТвЈә ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
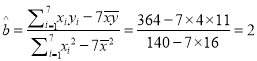 Ј¬
Ј¬ ![]() Ј¬
Ј¬
Фт![]() №ШУЪ
№ШУЪ![]() өДПЯРФ»Ш№й·ҪіМОӘ
өДПЯРФ»Ш№й·ҪіМОӘ![]() .
.
ЈЁ2Ј©ІОјУійҪұөДГҝО»№ЛҝН»сөГҪұЖ·Ҫр¶оОӘ![]() Ј¬
Ј¬ ![]() өД·ЦІјБРОӘ
өД·ЦІјБРОӘ
|
|
|
|
|
|
|
|
![]() ЈЁФӘЈ©.
ЈЁФӘЈ©.
УЙ![]() №ШУЪ
№ШУЪ![]() өД»Ш№йЦұПЯ·ҪіМ
өД»Ш№йЦұПЯ·ҪіМ![]() Ј¬ФӨІв
Ј¬ФӨІв![]() Кұ
Кұ![]() Ј¬
Ј¬ ![]() Кұ
Кұ![]() Ј¬
Ј¬ ![]() Кұ
Кұ![]() Ј¬
Ј¬
ФтҙЛҙО»о¶ҜІОјУійҪұөДИЛКэФјОӘ![]() ИЛЈ¬
ИЛЈ¬
![]() ЈЁФӘЈ©Ј¬
ЈЁФӘЈ©Ј¬
ЛщТФ№АјЖёГ·ЦөкФЪҙЛҙОійҪұ»о¶ҜҪбКшКұЛНіц![]() ФӘҪұЖ·.
ФӘҪұЖ·.


 НЁіЗС§өдД¬РҙДЬКЦПөБРҙр°ё
НЁіЗС§өдД¬РҙДЬКЦПөБРҙр°ё ҪрЕЖҪМёЁЕаУЕУЕСЎҫнЖЪД©іеҙМ100·ЦПөБРҙр°ё
ҪрЕЖҪМёЁЕаУЕУЕСЎҫнЖЪД©іеҙМ100·ЦПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Йи![]() Ул¶Ёөг
Ул¶Ёөг![]() өДҫаАләНЛьөҪЦұПЯ
өДҫаАләНЛьөҪЦұПЯ![]() өДҫаАлөДұИКЗіЈКэ
өДҫаАлөДұИКЗіЈКэ![]() Ј¬
Ј¬
ЈЁ1Ј©Зуөг![]() өД№мјЈЗъПЯ
өД№мјЈЗъПЯ![]() өД·ҪіМЈә
өД·ҪіМЈә
ЈЁ2Ј©№э¶Ёөг![]() өДЦұПЯ
өДЦұПЯ![]() Ҫ»ЗъПЯ
Ҫ»ЗъПЯ![]() УЪ
УЪ![]() БҪөгЈ¬ТФ
БҪөгЈ¬ТФ![]() ИэөгЈЁ
ИэөгЈЁ![]() ОӘЧшұкФӯөгЈ©ОӘ¶ҘөгЧчЖҪРРЛДұЯРО
ОӘЧшұкФӯөгЈ©ОӘ¶ҘөгЧчЖҪРРЛДұЯРО![]() ,Ифөг
,Ифөг![]() ёХәГФЪЗъПЯ
ёХәГФЪЗъПЯ![]() ЙПЈ¬ЗуЦұПЯ
ЙПЈ¬ЗуЦұПЯ![]() өД·ҪіМЈ®
өД·ҪіМЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіҪМУэ»ъ№№Лж»ъДіРЈ20ёц°ај¶Ј¬өчІйёч°а№ШЧўәәЧЦМэРҙҙуИьөДС§ЙъИЛКэЈ¬ёщҫЭЛщөГКэҫЭөДҫҘТ¶НјЈ¬ТФЧйҫаОӘ5Ҫ«КэҫЭ·ЦЧйіЙ[0Ј¬5Ј©Ј¬[5Ј¬10Ј©Ј¬[10Ј¬15Ј©Ј¬[15Ј¬20Ј©Ј¬[20Ј¬25Ј©Ј¬[25Ј¬30Ј©Ј¬[30Ј¬35Ј©Ј¬[35Ј¬40]КұЈ¬ЛщЧчөДЖөВК·ЦІјЦұ·ҪНјИзНјЛщКҫЈ¬ФтФӯКјҫҘТ¶НјҝЙДЬКЗЈЁ Ј© 
A.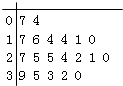
B.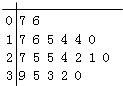
C.
D.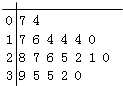
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҫӯПъЙМҫӯПъДіЦЦЕ©ІъЖ·Ј¬ФЪТ»ёцПъКЫјҫ¶ИДЪЈ¬ГҝКЫіц![]() ёГІъЖ·»сАыИу500ФӘЈ¬ОҙКЫіцөДІъЖ·Ј¬Гҝ
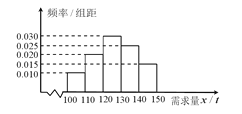
ёГІъЖ·»сАыИу500ФӘЈ¬ОҙКЫіцөДІъЖ·Ј¬Гҝ![]() ҝчЛр300ФӘЈ®ёщҫЭАъК·ЧКБПЈ¬өГөҪПъКЫјҫ¶ИДЪКРіЎРиЗуБҝөДЖөВК·ЦІјЦұНјЈ¬ИзНјЛщКҫЈ®ҫӯПъЙМОӘПВТ»ёцПъКЫјҫ¶И№әҪшБЛ
ҝчЛр300ФӘЈ®ёщҫЭАъК·ЧКБПЈ¬өГөҪПъКЫјҫ¶ИДЪКРіЎРиЗуБҝөДЖөВК·ЦІјЦұНјЈ¬ИзНјЛщКҫЈ®ҫӯПъЙМОӘПВТ»ёцПъКЫјҫ¶И№әҪшБЛ![]() ёГЕ©ІъЖ·Ј®ТФ
ёГЕ©ІъЖ·Ј®ТФ![]() ЈЁ
ЈЁ![]() Ј©ұнКҫПВТ»ёцПъКЫјҫ¶ИДЪөДКРіЎРиЗуБҝЈ¬
Ј©ұнКҫПВТ»ёцПъКЫјҫ¶ИДЪөДКРіЎРиЗуБҝЈ¬ ![]() ЈЁөҘО»ЈәФӘЈ©ұнКҫПВТ»ёцПъКЫјҫ¶ИДЪҫӯПъёГЕ©ІъЖ·өДАыИуЈ®
ЈЁөҘО»ЈәФӘЈ©ұнКҫПВТ»ёцПъКЫјҫ¶ИДЪҫӯПъёГЕ©ІъЖ·өДАыИуЈ®
ЈЁўсЈ©Ҫ«![]() ұнКҫОӘ
ұнКҫОӘ![]() өДәҜКэЈ»
өДәҜКэЈ»
ЈЁўтЈ©ёщҫЭЦұ·ҪНј№АјЖАыИу![]() І»ЙЩУЪ57000ФӘөДёЕВКЈ®
І»ЙЩУЪ57000ФӘөДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіСХБП№«ЛҫЙъІъ![]() Ўў
Ўў![]() БҪЦЦІъЖ·Ј¬ЖдЦРЙъІъГҝ¶Ц
БҪЦЦІъЖ·Ј¬ЖдЦРЙъІъГҝ¶Ц![]() ІъЖ·Ј¬РиТӘјЧИҫБП
ІъЖ·Ј¬РиТӘјЧИҫБП![]() ¶ЦЈ¬ТТИҫБП
¶ЦЈ¬ТТИҫБП![]() ¶ЦЈ¬ұыИҫБП
¶ЦЈ¬ұыИҫБП![]() ¶ЦЈ¬ЙъІъГҝ¶Ц
¶ЦЈ¬ЙъІъГҝ¶Ц![]() ІъЖ·Ј¬РиТӘјЧИҫБП
ІъЖ·Ј¬РиТӘјЧИҫБП![]() ¶ЦЈ¬ТТИҫБП
¶ЦЈ¬ТТИҫБП![]() ¶ЦЈ¬ұыИҫБП
¶ЦЈ¬ұыИҫБП![]() ¶ЦЈ¬ЗТёГ№«ЛҫТ»МмЦ®ДЪјЧЎўТТЎўұыИэЦЦИҫБПөДУГБҝ·ЦұрІ»і¬№э
¶ЦЈ¬ЗТёГ№«ЛҫТ»МмЦ®ДЪјЧЎўТТЎўұыИэЦЦИҫБПөДУГБҝ·ЦұрІ»і¬№э![]() ¶ЦЎў
¶ЦЎў![]() ¶ЦЎў
¶ЦЎў![]() ¶ЦЈ¬Из№ы
¶ЦЈ¬Из№ы![]() ІъЖ·өДАыИуОӘ
ІъЖ·өДАыИуОӘ![]() ФӘ/¶ЦЈ¬
ФӘ/¶ЦЈ¬ ![]() ІъЖ·өДАыИуОӘ
ІъЖ·өДАыИуОӘ![]() ФӘ/¶ЦЈ¬ФтёГСХБП№«ЛҫТ»МмДЪҝЙ»сөГөДЧоҙуАыИуОӘЈЁ Ј©
ФӘ/¶ЦЈ¬ФтёГСХБП№«ЛҫТ»МмДЪҝЙ»сөГөДЧоҙуАыИуОӘЈЁ Ј©
A. ![]() ФӘ B.
ФӘ B. ![]() ФӘ C.
ФӘ C. ![]() ФӘ D.
ФӘ D. ![]() ФӘ
ФӘ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЎчABCЦРЈ¬ТСЦӘ ![]() tanAtanB©ҒtanA©ҒtanB=
tanAtanB©ҒtanA©ҒtanB= ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЎПCөДҙуРЎЈ»
ЈЁ2Ј©ЙиҪЗAЈ¬BЈ¬CөД¶ФұЯТАҙООӘaЈ¬bЈ¬cЈ¬Ифc=2Ј¬ЗТЎчABCКЗИсҪЗИэҪЗРОЈ¬Зуa2+b2өДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЎҫЙҪ¶«КЎКөСйЦРС§2017ҪмёЯИэөЪТ»ҙОХп¶ПЎҝТСЦӘНЦФІ![]() Јә
Јә![]() өДУТҪ№өг
өДУТҪ№өг![]() Ј¬№эөг
Ј¬№эөг![]() ЗТУлЧшұкЦбІ»ҙ№ЦұөДЦұПЯУлНЦФІҪ»УЪ
ЗТУлЧшұкЦбІ»ҙ№ЦұөДЦұПЯУлНЦФІҪ»УЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬өұЦұПЯ
БҪөгЈ¬өұЦұПЯ![]() ҫӯ№эНЦФІөДТ»ёц¶ҘөгКұЖдЗгРұҪЗЗЎәГОӘ
ҫӯ№эНЦФІөДТ»ёц¶ҘөгКұЖдЗгРұҪЗЗЎәГОӘ![]() Ј®
Ј®
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©Йи![]() ОӘЧшұкФӯөгЈ¬ПЯ¶О
ОӘЧшұкФӯөгЈ¬ПЯ¶О![]() ЙПКЗ·сҙжФЪөг
ЙПКЗ·сҙжФЪөг![]() Ј¬К№өГ
Ј¬К№өГ![]() ЈҝИфҙжФЪЈ¬ЗуіцКөКэ
ЈҝИфҙжФЪЈ¬ЗуіцКөКэ![]() өДИЎЦө·¶О§Ј»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
өДИЎЦө·¶О§Ј»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ¶ҜЦұПЯ![]() №эөг
№эөг![]() Ј¬ЗТУлФІ
Ј¬ЗТУлФІ![]() Ҫ»УЪ
Ҫ»УЪ![]() Ўў
Ўў![]() БҪөгЈ®
БҪөгЈ®
ЈЁ1Ј©ИфЦұПЯ![]() өДРұВКОӘ
өДРұВКОӘ![]() Ј¬Зу
Ј¬Зу![]() өДГж»эЈ»
өДГж»эЈ»
ЈЁ2Ј©ИфЦұПЯ![]() өДРұВКОӘ
өДРұВКОӘ![]() Ј¬өг
Ј¬өг![]() КЗФІ
КЗФІ![]() ЙПИОТвТ»өгЈ¬Зу
ЙПИОТвТ»өгЈ¬Зу![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁ3Ј©КЗ·сҙжФЪТ»ёц¶Ёөг![]() ЈЁІ»Н¬УЪөг
ЈЁІ»Н¬УЪөг![]() Ј©Ј¬¶ФУЪИОТвІ»Ул
Ј©Ј¬¶ФУЪИОТвІ»Ул![]() ЦбЦШәПөДЦұПЯ
ЦбЦШәПөДЦұПЯ![]() Ј¬¶јУР
Ј¬¶јУР![]() ЖҪ·Ц
ЖҪ·Ц![]() Ј¬ИфҙжФЪЈ¬Зуіц¶Ёөг
Ј¬ИфҙжФЪЈ¬Зуіц¶Ёөг![]() өДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
өДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЎчABCЦРЈ¬ИфacosA©ҒbcosB=0Ј¬ФтИэҪЗРОөДРОЧҙКЗЈЁ Ј©
A.өИСьИэҪЗРО
B.ЦұҪЗИэҪЗРО
C.өИСьЦұҪЗИэҪЗРО
D.өИСьИэҪЗРО»тЦұҪЗИэҪЗРО
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com