
【题目】(本题满分16分)已知函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的切线,求
图象的切线,求![]() 的最小值;
的最小值;
(3)当![]() 时,若
时,若![]() 与
与![]() 的图象有两个交点
的图象有两个交点![]() ,求证:
,求证: ![]()
![]() .(取
.(取![]() 为
为![]() ,取
,取![]() 为
为![]() ,取
,取![]() 为
为![]() )
)
【答案】(1)![]() (2)
(2)![]() .(3)详见解析
.(3)详见解析
【解析】试题分析:(1)由题意得对![]() ,
, ![]() 恒成立,即
恒成立,即![]() ,∵
,∵![]() ,∴
,∴![]() (2)设切点
(2)设切点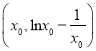 ,由导数几何意义得
,由导数几何意义得![]() ,
, ![]() ,令
,令![]() ,则
,则![]() ,问题就转化为利用导数求最值:由
,问题就转化为利用导数求最值:由![]() 得当
得当![]() 时 ,
时 , ![]() ,
, ![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,故
,故![]() 的最小值为
的最小值为![]() .(3)本题较难,难点在于构造函数.先根据等量关系消去参数a:由题意知
.(3)本题较难,难点在于构造函数.先根据等量关系消去参数a:由题意知![]() ,
, ![]() ,两式相加得
,两式相加得![]() ,两式相减得
,两式相减得![]() ,即
,即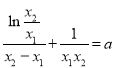 ,
,
∴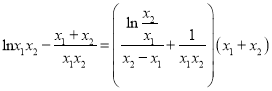 ,即
,即![]() ,为研究等式右边范围构造函数
,为研究等式右边范围构造函数![]() ,易得
,易得![]() 在
在![]() 上单调递增,因此当
上单调递增,因此当![]() 时,有
时,有![]() 即
即![]() ,所以
,所以![]() ,再利用基本不等式进行放缩:
,再利用基本不等式进行放缩: 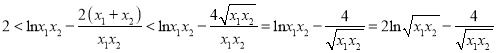 ,
,
即![]() ,再一次构造函数
,再一次构造函数![]() ,易得其在
,易得其在![]() 上单调递增,而
上单调递增,而![]() ,因此
,因此![]() ,即
,即![]() .
.
试题解析:解:(1)![]()
![]() ,则
,则![]() ,
,
∵![]() 在
在![]() 上单调递增,∴对
上单调递增,∴对![]() ,都有
,都有![]() ,
,
即对![]() ,都有
,都有![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() . 4分
. 4分
(2)设切点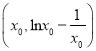 ,则切线方程为
,则切线方程为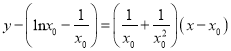 ,
,
即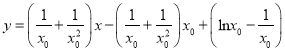 ,亦即
,亦即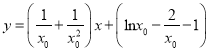 ,
,
令![]() ,由题意得
,由题意得![]() , 7分
, 7分
令![]() ,则
,则![]() ,
,
当![]() 时 ,
时 , ![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,故
,故![]() 的最小值为
的最小值为![]() . 10分
. 10分
(3)由题意知![]() ,
, ![]() ,
,
两式相加得![]() ,两式相减得
,两式相减得![]() ,
,
即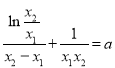 ,∴
,∴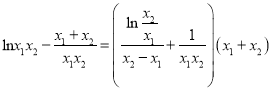 ,
,
即![]() , 12分
, 12分
不妨令![]() ,记
,记![]() ,令
,令![]() ,则
,则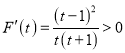 ,
,
∴![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
∴![]() ,则
,则![]() ,∴
,∴![]() ,
,
又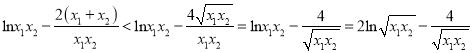 ,
,
∴![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
∴![]() ,则
,则![]() ,即
,即![]() .
.
16分


科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q≠1,则下面说法中不正确的是( )
A.{an+2+an}是等比数列
B.对于k∈N* , k>1,ak﹣1+ak+1≠2ak
C.对于n∈N* , 都有anan+2>0
D.若a2>a1 , 则对于任意n∈N* , 都有an+1>an
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(x1 , f(x1),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() .
.
(1)求函数f(x)的解析式;
(2)当x∈[0, ![]() ]时,求函数f(x)的单调递增区间;
]时,求函数f(x)的单调递增区间;
(3)当x∈[0, ![]() ]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m﹣2)x+1=0无实根,若“p或q”真“p且q”为假,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年推出一种新型家用轿车,购买时费用为14.4万元,每年应交付保险费、养路费及汽车油费共0.7万元,
汽车维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费用均比上一年增加0.2万元
(1)设该辆轿车使用n年的总费用(包括购买费用,保险费,养路费,汽车费及维修费)为f(n),求f(n)的表达式.
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,an+1=(1+ ![]() )an+
)an+ ![]() .
.
(1)设bn= ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD= ![]() ,E是BC中点,点Q在侧棱PC上.
,E是BC中点,点Q在侧棱PC上. 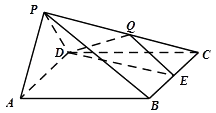
(1)求证:AD⊥PB;
(2)若Q是PC中点,求二面角E﹣DQ﹣C的余弦值;
(3)若 ![]() ,当PA∥平面DEQ时,求λ的值.
,当PA∥平面DEQ时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ![]() ),左右焦点为F1、F2 , 右顶点为A,上顶点为B,且|AB|=
),左右焦点为F1、F2 , 右顶点为A,上顶点为B,且|AB|= ![]() |F1F2|.
|F1F2|.
(1)求椭圆E的方程;
(2)直线l:y=﹣x+m与椭圆E交于C、D两点,与以F1、F2为直径的圆交于M、N两点,且 ![]() =
= ![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com