
【题目】给出下列命题:
①△ABC中角A,B,C的对边分别是a,b,c,若a>b,则cosA<cosB,cos2A<cos2B;
②a,b∈R,若a>b,则a3>b3;
③若a<b,则 ![]() <
< ![]() ;
;
④设等差数列{an}的前n项和为Sn , 若S2016﹣S1=1,则S2017>1.
其中正确命题的序号是 .
【答案】①②④
【解析】解:①,△ABC中角A,B,C的对边分别是a,b,c,若a>b,由正弦定理得sinA>sinB,利用同角三角函数的基本关系可得cosA<cosB,
由sinA>sinB>0,得sin2A>sin2B,∴1﹣2sin2A<1﹣2sin2B,则cos2A<cos2B,故①正确;
②,a,b∈R,若a>b,由不等式的性质得a3>b3 , 故②正确;
③,取a=1,b=3,x=1,满足a<b, ![]() >
> ![]() ,故③错误;
,故③错误;
④,等差数列{an}的前n项和为Sn , 若S2016﹣S1=1,则a2+a3+…+a2016=1,
∴2015a1+(d+2d+…+2015d)=1,则 ![]() ,
,
∴ ![]() ,即
,即 ![]() ,则S2017=2017
,则S2017=2017 ![]() >1,故④正确.
>1,故④正确.
∴正确命题的个数是①②④.
所以答案是:①②④.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=2,an+1= ![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)证明:数列{ ![]() }是等比数列;
}是等比数列;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=x2-x-15,且|x-a|<1,
(1)解不等式![]() ;
;
(2)求证:|f(x)-f(a)|<2(|a|+1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是矩形,侧面PAD丄底面ABCD,∠APD= ![]() . (I )求证:平面PAB丄平面PCD;
. (I )求证:平面PAB丄平面PCD;
(II)如果AB=BC,PB=PC,求二面角B﹣PC﹣D的余弦值.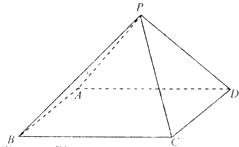
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4个不同的小球,4个不同的盒子,现要把球全部放进盒子内.
(1)恰有1个盒子不放球,共有多少种方法?
(2)恰有2个盒子不放球,共有多少种方法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com