
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: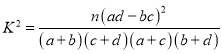 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
科目:高中数学 来源: 题型:
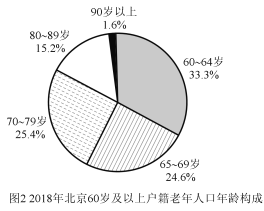
【题目】目前,我国老年人口比例不断上升,造成日趋严峻的人口老龄化问题.2019年10月12日,北京市老龄办、市老龄协会联合北京师范大学中国公益研究院发布《北京市老龄事业发展报告(2018)》,相关数据有如下图表.规定年龄在15岁至59岁为“劳动年龄”,具备劳动力,60岁及以上年龄为“老年人”,据统计,2018年底北京市每2.4名劳动力抚养1名老年人.
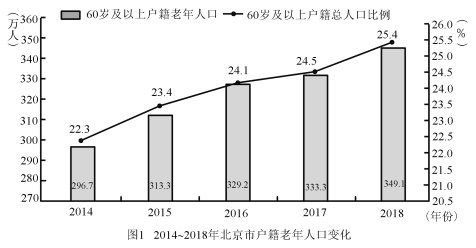
(Ⅰ)请根据上述图表计算北京市2018年户籍总人口数和北京市2018年的劳动力数;(保留两位小数)
(Ⅱ)从2014年起,北京市老龄人口与年份呈线性关系,比照2018年户籍老年人人口年龄构成,预计到2020年年底,北京市90以上老人达到多少人?(精确到1人)
(附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: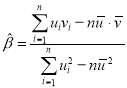 ,
,![]() .
.![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间![]() 岁之间,对区间
岁之间,对区间![]() 岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:

组数 | 分组 | 人数 |
第一组 |
| 2 |
第二组 |
| a |
第三组 |
| 5 |
第四组 |
| 4 |
第五组 |
| 3 |
第六组 |
| 2 |
(1)求a的值并画出频率分布直方图;
(2)从被调查的20人且年龄在![]() 岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间
岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间![]() 岁年龄段的人数为X,求随机变量X的分布列及数学期望.
岁年龄段的人数为X,求随机变量X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,点
内一个定点,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与半径
的垂直平分线与半径![]() 相交于点
相交于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)给定点![]() ,设直线
,设直线![]() 不经过点
不经过点![]() 且与轨迹
且与轨迹![]() 相交于
相交于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为直径的圆过点
为直径的圆过点![]() .证明:直线
.证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com