练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】椭圆 的左、右焦点分别为F1 ， F2 ， 弦AB过F1 ， 若△ABF2的内切圆周长为π，A，B两点的坐标分别为（x1 ， y1），（x2 ， y2），则|y1﹣y2|的值为 ．

    【答案】
    【解析】解：椭圆 中，a2=25且b2=16，∴a=5，c= ，∴椭圆的焦点分别为F1（﹣3，0）、F2（3，0），

    设△ABF2的内切圆半径为r，

    ∵△ABF2的内切圆周长为π，∴r= ，

    根据椭圆的定义，得|AB|+|AF2|+|BF2|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=4a=20．

    ∴△ABF2的面积S= （|AB|+|AF2|+|BF2|）×r= ×20× =5，

    又∵△ABF2的面积S= = ×|y1|×|F1F2|+ ×|y2|×|F1F2|

    = ×（|y1|+|y2|）×|F1F2|=4|y2﹣y1|（A、B在x轴的两侧），

    ∴4|y1﹣y2|=5，解得|y1﹣y2|= ．

    所以答案是： ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：m），修建此矩形场地围墙的总费用为y（单位：元）． （Ⅰ）将y表示为x的函数：
    （Ⅱ）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对任意实数x，[x]表示不超过x的最大整数，如[3.6]=3，[﹣3.6]=﹣4，关于函数f（x）=[ ﹣[ ]]，有下列命题： ①f（x）是周期函数；
    ②f（x）是偶函数；
    ③函数f（x）的值域为{0，1}；
    ④函数g（x）=f（x）﹣cosπx在区间（0，π）内有两个不同的零点，
    其中正确的命题为（把正确答案的序号填在横线上）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=﹣x3+ax2+bx+c的导数f'（x）满足f'（﹣1）=0，f'（2）=9．
    （1）求f（x）的单调区间；
    （2）f（x）在区间[﹣2，2]上的最大值为20，求c的值．
    （3）若函数f（x）的图象与x轴有三个交点，求c的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了培养学生的数学建模和应用能力，某校组织了一次实地测量活动，如图，假设待测量的树木 的高度 ，垂直放置的标杆 的高度 ，仰角 三点共线），试根据上述测量方案，回答如下问题：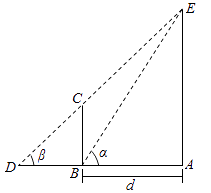

    （1）若测得 ，试求 的值；
    （2）经过分析若干测得的数据后，大家一致认为适当调整标杆到树木的距离 （单位：）使 与 之差较大时，可以提高测量的精确度.若树木的实际高为 ，试问 为多少时， 最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线 ，方程x2+y2﹣2mx﹣2y+m+3=0表示圆．
    （Ⅰ）求实数m的取值范围；
    （Ⅱ）当m=﹣2时，试判断直线l与该圆的位置关系，若相交，求出相应弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一个科研小组有4位男组员和2位女组员，其中一位男组员和一位女组员不会英语，其他组员都会英语，现在要用抽签的方法从中选出两名组员组成一个科研攻关小组．
    （Ⅰ）求组成攻关小组的成员是同性的概率；
    （Ⅱ）求组成攻关小组的成员中有会英语的概率；
    （Ⅲ）求组成攻关小组的成员中有会英语并且是异性的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a∈R，解关于x的不等式（a﹣1）x2+（2a+3）x+a+2＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列 的前 n 项和为 Sn ，且(3-m)Sn+2man=m+3() ，其中 m 为常数，且 .
    ①求证： 是等比数列；
    ②若数列 的公比为q=f(m) ，数列 {bn} 满足 b1=a1 ， ，求证： 为等差数列.

    查看答案和解析>>

    同步练习册答案