
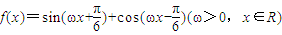 ,且该函数图象相邻两对称轴间的距离为
,且该函数图象相邻两对称轴间的距离为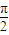 .
.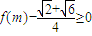 成立,求实数m的取值范围.
成立,求实数m的取值范围.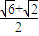 sin(ωx+
sin(ωx+ ),由该函数图象相邻两对称轴间的距离为
),由该函数图象相邻两对称轴间的距离为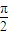 ,可得函数f(x)的最小正周期为π,由此求得ω=2.
,可得函数f(x)的最小正周期为π,由此求得ω=2.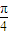 )≥
)≥ ,故有 2kπ-
,故有 2kπ-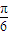 ≤2m+
≤2m+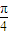 )≤2kπ+
)≤2kπ+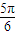 ,k∈z.由此解得实数m的取值范围.
,k∈z.由此解得实数m的取值范围.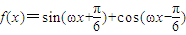 =
=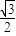 sinωx+
sinωx+ cosωx+
cosωx+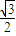 cosωx+
cosωx+ sinωx
sinωx (sinωx+cosωx)=
(sinωx+cosωx)=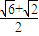 sin(ωx+
sin(ωx+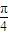 ).
). ,∴函数f(x)的最小正周期为π,
,∴函数f(x)的最小正周期为π,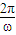 =π,ω=2,f(x)=
=π,ω=2,f(x)=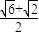 sin(2x+
sin(2x+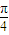 ).
).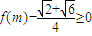 成立,∴
成立,∴ sin(2m+
sin(2m+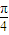 )≥
)≥ ,
,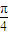 )≥
)≥ .
.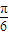 ≤2m+
≤2m+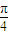 )≤2kπ+
)≤2kπ+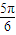 ,k∈z.解得 kπ-
,k∈z.解得 kπ- ≤m≤kπ+
≤m≤kπ+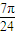 ,k∈z.
,k∈z.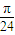 ,kπ+
,kπ+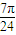 ]k∈z.
]k∈z.

 综合自测系列答案
综合自测系列答案科目:高中数学 来源:山东省鱼台二中2011-2012学年高一上学期期末模拟考试数学试题 题型:044
已知函数![]() 的图象与y轴相交于点M
的图象与y轴相交于点M![]() ,且该函数的最小正周期为
,且该函数的最小正周期为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)已知点![]() ,点P是该函数图象上一点,点
,点P是该函数图象上一点,点![]() 是PA的中点,当
是PA的中点,当![]() ,
,![]() 时,求x0的值.
时,求x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 =(sin(ωx+?),2),
=(sin(ωx+?),2), =(1,cos(ωx+?))
=(1,cos(ωx+?))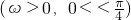 ,函数f(x)=(
,函数f(x)=( +
+ )•(
)•( -
- )的图象过点
)的图象过点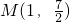 ,且该函数相邻两条对称轴间的距离为2.
,且该函数相邻两条对称轴间的距离为2. =
=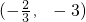 平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.
平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.查看答案和解析>>
科目:高中数学 来源:2011年湖北省武汉市武昌区高三五月调考数学试卷(理科)(解析版) 题型:解答题
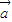 =(sin(ωx+ϕ),2),
=(sin(ωx+ϕ),2),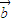 =(1,cos(ωx+ϕ))
=(1,cos(ωx+ϕ))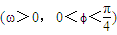 ,函数f(x)=(
,函数f(x)=(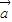 +
+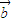 )•(
)•(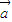 -
-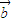 )的图象过点
)的图象过点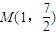 ,且该函数相邻两条对称轴间的距离为2.
,且该函数相邻两条对称轴间的距离为2.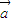 =
=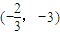 平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.
平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com