
分析 (1)由g(x)=x2+bsinx-2+2得g(x)=x2+bsinx,利用g(-x)=g(x),求函数f(x)的解析式;
(2)已知函数h(x)=f(x)+2(x+1)+alnx在区间(0,1)上单调,有h'(x)≥0或h'(x)≤0恒成立,分离参数,求最值,即可求实数a的取值范围.
解答 解:(1)由g(x)=x2+bsinx-2+2得g(x)=x2+bsinx
∵g(-x)=g(x)
∴x2-bsinx=x2+bsinx
∴bsinx=0⇒sinx=0或 b=0
故f(x)=x2-2
(2)由 h(x)=x2-2+2(x+1)+alnx得h(x)=x2+2x+alnx(x>0),
$h'(x)=2x+2+\frac{a}{x}$(x>0)
∵h(x)在区间(0,1)上单调,
∴有h'(x)≥0或h'(x)≤0恒成立
即2x2+2x+a≥0或2x2+2x+a≤0,
∴a≥-2x2-2x或a≤-2x2-2x
设t=-2x2-2x,当0<x<1时,-4<t<0,
∴a≥0或a≤-4
∴实数a的取值范围是(-∞,-4]∪[0,+∞).
点评 本题考查利用导数知识的应用,考查函数的解析式,考查运算求解能力,推理论证能力;考查化归与转化思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{e}$ | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{{e}^{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 类别 | 1号广告 | 2号广告 | 3号广告 | 4号广告 |
| 广告次数 | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.
在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:选择题
在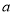 和
和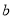 两数之间插入5个数,使他们与
两数之间插入5个数,使他们与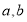 组成等差数列,则该数列的公差为( )
组成等差数列,则该数列的公差为( )
A.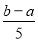 B.
B.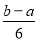 C.
C.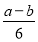 D.
D.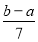
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com