练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数且）.

    （1）求的定义域；

    （2）讨论函数的单调性.

    【答案】（1）当时， 定义域是；当时，定义域是；（2）当时，在（0，+∞）上是增函数，当时，在（-∞，0）上也是增函数.

    【解析】试题分析：（1）要使函数有意义，则有，讨论两种情况，分别根据指数函数的性质求解不等式即可；（2）当时，是增函数，是增函数；当时，.是减函数，是减函数，进而可得函数的单调性.

    试题解析：（1）令，即，

    当时，的解集是（0，+∞）；

    当时，的解集是（-∞，0）；

    所以，当时，的定义域是（0，+∞）；

    当时，的定义域是（-∞，0）.

    （2）当时，是增函数，是增函数，从而函数在（0，+∞）上是增函数，

    同理可证：当时，函数在（-∞，0）上也是增函数.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】四棱柱中，底面为正方形， 平面为棱的中点， 为棱的中点， 为棱的中点.

    （1）证明：平面平面；

    （2）若，棱上有一点，且，使得二面角的余弦值为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知圆的方程为，点的坐标为.

    （1）求过点且与圆相切的直线方程；

    （2）过点任作一条直线与圆交于不同两点，，且圆交轴正半轴于点，求证：直线与的斜率之和为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f (x)在R上可导，其导函数为f ′(x)，且函数f (x)在x＝－2处取得极大值，则函数y＝f ′(x)的图象可能是

    A. B.

    C. D.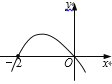

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为自然对数的底数)．

    （1）若,求函数的单调区间；

    （2）若,且方程在内有解,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是由一平面内的个向量组成的集合．若，且的模不小于中除外的所有向量和的模．则称是的极大向量.有下列命题：

    ①若中每个向量的方向都相同，则中必存在一个极大向量；

    ②给定平面内两个不共线向量，在该平面内总存在唯一的平面向量，使得中的每个元素都是极大向量；

    ③若中的每个元素都是极大向量，且中无公共元素，则中的每一个元素也都是极大向量．

    其中真命题的序号是_______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项等差数列的前项和是若，且成等比数列.

    (1)求数列的通项公式；

    (2)记的前项和是，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，过点的直线与抛物线交于，两点，线段的垂直平分线交轴于点，若，则点的横坐标为（ ）

    A. 5 B. 4 C. 3 D. 2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（12分）

    一只药用昆虫的产卵数y（单位：个）与一定范围内的温度（单位：℃）有关，现收集了该种药用昆虫的6组观测数据如下表所示.

    经计算得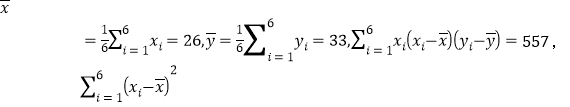

    ，线性回归模型的残差平方和

    ，其中分别为观测数据中的温度和产卵数，

    （1）若用线性回归模型，求的回归方程（结果精确到0.1）.

    （2）若用非线性回归模型预测当温度为35℃时，该种药用昆虫的产卵数（结果取整数）.

    附：一组数据，其回归直线的斜率和截距的最小二乘估计分别为.

    查看答案和解析>>

    同步练习册答案