
【题目】已知数列{an}的前n项和为Sn , 且满足an=2Sn+1(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
【答案】解:(Ⅰ)当n=1时,a1=2S1+1=2a1+1,解得a1=﹣1.
当n≥2时,an=2Sn+1,an﹣1=2Sn﹣1+1,两式相减得an﹣an﹣1=2an , 化简得an=﹣an﹣1 ,
所以数列{an}是首项为﹣1,公比为﹣1的等比数列,
可得 ![]() .
.
(Ⅱ)由(Ⅰ)得 ![]() ,
,
当n为偶数时,bn﹣1+bn=2, ![]() ;
;
当n为奇数时,n+1为偶数,Tn=Tn+1﹣bn+1=(n+1)﹣(2n+1)=﹣n.
所以数列{bn}的前n项和 ![]()
【解析】(Ⅰ)当n=1时,a1=2S1+1=2a1+1,解得a1 . 当n≥2时,an=2Sn+1,an﹣1=2Sn﹣1+1,两式相减得an﹣an﹣1=2an , 利用等比数列的通项公式即可得出.(Ⅱ)由(Ⅰ)得 ![]() ,对n分类讨论:当n为偶数时,bn﹣1+bn=2,可得Tn;当n为奇数时,n+1为偶数,Tn=Tn+1﹣bn+1 .
,对n分类讨论:当n为偶数时,bn﹣1+bn=2,可得Tn;当n为奇数时,n+1为偶数,Tn=Tn+1﹣bn+1 .
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex﹣2x﹣2a,且a∈[1,2],设函数f(x)在区间[0,ln2]上的最小值为m,则m的取值范围是( )
A.[﹣2,﹣2ln2]
B.[﹣2,﹣ ![]() ]
]
C.[﹣2ln2,﹣1]
D.[﹣1,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C1的参数方程为 ![]() (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,与直角坐标系xoy取相同的单位长度建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ.
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,与直角坐标系xoy取相同的单位长度建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ﹣4sinθ.
(1)化曲线C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C2与x轴的一个交点的坐标为P(m,0)(m>0),经过点P作斜率为1的直线,l交曲线C2于A,B两点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2x+ ![]() )(x∈[0,
)(x∈[0, ![]() ]),若方程f(x)=a恰好有三个根,分别为x1 , x2 , x3(x1<x2<x3),则x1+x2+x3的取值范围是( )
]),若方程f(x)=a恰好有三个根,分别为x1 , x2 , x3(x1<x2<x3),则x1+x2+x3的取值范围是( )
A.[ ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() )
)
C.[ ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx﹣3x2﹣11x.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)≤(a﹣3)x2+(2a﹣13)x﹣2恒成,求整数a的最小值;
(3)若正实数x1 , x2满足f(x1)+f(x2)+4(x ![]() +x
+x ![]() )+12(x1+x2)=4,证明:x1+x2≥2.
)+12(x1+x2)=4,证明:x1+x2≥2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2sinθ.
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2sinθ.
(Ⅰ)判断直线l与圆C的交点个数;
(Ⅱ)若圆C与直线l交于A,B两点,求线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面ADC∥平面A1B1C1 , B为线段AD的中点,△ABC≈△A1B1C1 , 四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A= ![]() ,M为棱A1C1的中点.
,M为棱A1C1的中点.
(I)若N为线段DC1上的点,且直线MN∥平面ADB1A1 , 试确定点N的位置;
(Ⅱ)求平面MAD与平面CC1D所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( ) 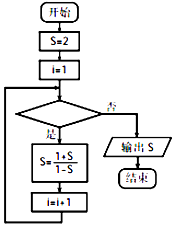
A.i≤2015?
B.i≤2016?
C.i≤2017?
D.i≤2018?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,”延迟退休“已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com