
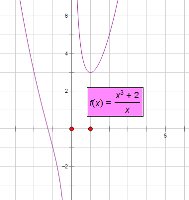
【题目】已知函数![]() 的图象与函数
的图象与函数![]() 的图象有三个不同的交点
的图象有三个不同的交点![]() 、
、![]() 、
、![]() ,其中
,其中![]() .给出下列四个结论: ①
.给出下列四个结论: ①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中,正确结论的个数有( )个
.其中,正确结论的个数有( )个
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析:由题意,函数![]() 的图象与函数
的图象与函数![]() 的图象有三个不同的交点,转化为方程
的图象有三个不同的交点,转化为方程![]() 有三个不同的实数解,进而函数
有三个不同的实数解,进而函数![]() 与
与![]() 的图象有三个不同的交点,利用导数求解函数
的图象有三个不同的交点,利用导数求解函数![]() 的单调性和极值,即可得到答案.
的单调性和极值,即可得到答案.
详解:由题意,函数![]() 的图象与函数
的图象与函数![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
即方程![]() ,由三个不同的实数解,即
,由三个不同的实数解,即![]() 有三个不同的实数解,
有三个不同的实数解,
即函数![]() 与
与![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
又由![]() ,
,
当![]() 或
或![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
其图象如图所示,且当![]() 时,
时,![]() ,
,
要使得函数![]() 与
与![]() 的图象有三个不同的交点,则
的图象有三个不同的交点,则![]() ,所以①正确的;
,所以①正确的;
当![]() 时,即
时,即![]() ,解得
,解得![]() 或
或![]() ,
,
所以当![]() 时,则
时,则![]() 所以②是正确的;
所以②是正确的;
结合图象可得![]() ,所以③是正确的;
,所以③是正确的;
又由![]() ,整理得
,整理得![]() ,
,
又因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
结合③可知![]() ,所以④是错误的,故选C.
,所以④是错误的,故选C.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,△PBC为等边三角形,点O为BC的中点,AC⊥PB,平面PBC⊥平面ABC.

(1)求直线PB和平面ABC所成的角的大小;
(2)求证:平面PAC⊥平面PBC;
(3)已知E为PO的中点,F是AB上的点,AF=![]() AB.若EF∥平面PAC,求
AB.若EF∥平面PAC,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣a(lnx+x).
(1)若函数f(x)恒有两个零点,求a的取值范围;
(2)若对任意x>0,恒有不等式f(x)≥1成立. ①求实数a的值;
②证明:x2ex>(x+2)lnx+2sinx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:

附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行理科、文科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.
分组 | 频数 | 频率 | 分组 | 频数 | 频率 | |
[135,150] | 8 | 0.08 | [135,150] | 4 | 0.04 | |
[120,135) | 17 | 0.17 | [120,135) | 18 | 0.18 | |
[105,120) | 40 | 0.4 | [105,120) | 37 | 0.37 | |
[90,105) | 21 | 0.21 | [90,105) | 31 | 0.31 | |
[75,90) | 12 | 0. 12 | [75,90) | 7 | 0.07 | |
[60,75) | 2 | 0.02 | [60,75) | 3 | 0.03 | |
总计 | 100 | 1 | 总计 | 100 | 1 |
理科 文科
(Ⅰ)根据数学成绩的频率分布表,求文科数学成绩的中位数的估计值;(精确到0.01)
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:
数学成绩 | 数学成绩<120分 | 合计 | |
理科 | |||
文科 | |||
合计 | 200 |
参考公式与临界值表: ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程是  (t是参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.曲线C的极坐标方程为ρ=4cos(θ+
(t是参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.曲线C的极坐标方程为ρ=4cos(θ+ ![]() ).
).
(1)判断直线l与曲线C的位置关系;
(2)过直线l上的点作曲线C的切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点M的极坐标为 ![]() ,圆C的参数方程为
,圆C的参数方程为 ![]() (α为参数).
(α为参数).
(1)直线l过M且与圆C相切,求直线l的极坐标方程;
(2)过点P(0,m)且斜率为 ![]() 的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com