练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知角θ的终边过点（4，-3），则tanθ=$-\frac{3}{4}$，$\frac{{sin（θ+{{90}°}）+cosθ}}{{sinθ-cos（θ-{{180}°}）}}$=8．

    分析 直接利用任意角的三角函数的定义即可求解tanθ，利用诱导公式，同角三角函数基本关系式化简所求即可 计算得解．

    解答 解：∵角θ终边上一点P（4，-3），
    ∴由三角函数的定义可得tanθ=$-\frac{3}{4}$，
    ∴$\frac{{sin（θ+{{90}°}）+cosθ}}{{sinθ-cos（θ-{{180}°}）}}$=$\frac{cosθ+cosθ}{sinθ-（-cosθ）}$=$\frac{2}{tanθ+1}$=8，
    故答案为：$-\frac{3}{4}$，8．

    点评 本题考查任意角的三角函数的定义，诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，属于基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知函数y=f（x）是R上的可导函数，当x≠0时，有$f'（x）+\frac{f（x）}{x}＞0$，则函数$F（x）=x•f（x）-\frac{1}{x}$的零点个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

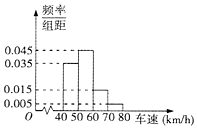    5．某市交管部门对一路段限速60km/h，为调查违章情况，对经过该路段的300辆汽车进行检测，将所得数据按[40，50），[50.60），[60，70），[70，80）（所有车辆的车速均在[40，80]内）分成四组，绘制成如图所示的频率分布直方图．
    （1）若用分层抽样的方法，从这300辆车中抽取20辆，则违章车有多少辆？其中多少辆车的车速不低于70km/h？
    （2）用此次检测结果估计全市车辆的违章情况，若随机抽取3辆车．
    （i）求这3辆车中违章车辆数ξ的分布列及期望；
    （ii）假如这3辆车都是违章车辆，从中随机抽取1辆，求其车速不低于70km．h的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知$f（α）=\frac{{cos（{\frac{π}{2}+α}）•cos（{2π-α}）•sin（{\frac{3π}{2}-α}）}}{{sin（{-π-α}）•sin（{\frac{3π}{2}+α}）}}$，
    （1）化简f（α）；
    （2）若α是第三象限角，且$sinα=-\frac{1}{5}$，求f（α）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知二次函数f（x）=ax2+bx+c，其中常数a，b，c∈R．
    （1）若f（3）=f（-1）=-5，且f（x）的最大值是3，求函数f（x）的解析式；
    （2）a=1，若对任意的x1，x2∈[-1，1]，有|f（x1）-f（x2）|≤4，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．高一年级有14个班，每个班学生的学号都是1～50，为了交流学习经验，要求各班学号为26的学生参加交流活动，这里运用的抽样方法是（　　）
    A．抽签法B．分层抽样C．系统抽样D．随机数表法

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．根据条件求双曲线的标准方程．
    （1）实轴长为8，离心率5，焦点在y轴上；
    （2）焦距为26，两顶点坐标为（0，-5），（0，5）；
    （3）渐近线方程为y=±x，且过点M（2，3）；
    （4）渐近线方程为y=$±\frac{3}{4}$x，且经过点（-2，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

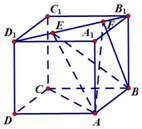    4．如图所示，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F，且$EF=\frac{{\sqrt{2}}}{2}$，则下列结论中正确的是①②③④．
    ①EF∥平面ABCD；
    ②平面ACF⊥平面BEF；
    ③三棱锥E-ABF的体积为定值；
    ④存在某个位置使得异面直线AE与BF成角30o．

    查看答案和解析>>

    同步练习册答案