
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() .
.
![]() 若
若![]() 的最大值为0,记
的最大值为0,记![]() ,求
,求![]() 的值;
的值;
![]() 当
当![]() 时,记不等式
时,记不等式![]() 的解集为M,求函数
的解集为M,求函数![]() ,
,![]() 的值域
的值域![]() 是自然对数的底数
是自然对数的底数![]() ;
;
![]() 当
当![]() 时,讨论函数
时,讨论函数![]() 的零点个数.
的零点个数.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin(x+ ![]() )﹣
)﹣ ![]() cos2x+
cos2x+ ![]() ,x∈R.
,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在闭区间[﹣ ![]() ,
, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥A﹣BCD及其侧视图、俯视图如图所示,设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP. 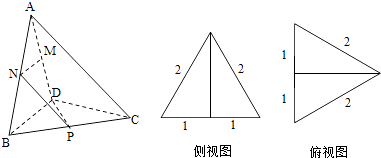
(1)证明:P是线段BC的中点;
(2)求二面角A﹣NP﹣M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com