
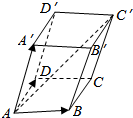
 在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系.
在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系. 分析 利用向量加法法则求解.
解答 解:在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,
$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$=$\overrightarrow{AC}$+$\overrightarrow{C{C}^{'}}$=$\overrightarrow{A{C}^{'}}$,
$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$=$\overrightarrow{A{B}^{'}}+\overrightarrow{{B}^{'}{C}^{'}}$=$\overrightarrow{A{C}^{'}}$,
∴向量加法运算满足交换律及结合律.
一般地,三个不共面的向量的和可以与分别以这三个向量为边的平行六面体的对角线建立起联系.
点评 本题考查向量加法运算,是基础题,解题时要认真审题,注意向量加法法则的合理运用.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{10\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {2,4} | C. | {1,2,4,5,6} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平面内的任意两个向量都共线 | B. | 空间的任意三个向量都不共面 | ||
| C. | 空间的任意两个向量都共面 | D. | 空间的任意三个向量都共面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com