
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,O是AD的中点.
,O是AD的中点.
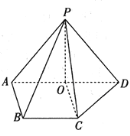
(1)在线段PA上找一点E,使得![]() 平面PCD,并证明;
平面PCD,并证明;
(2)在(1)的条件下,若![]() ,求平面OBE与平面POC所成的锐二面角的余弦值.
,求平面OBE与平面POC所成的锐二面角的余弦值.
【答案】(1)E是线段PA的中点,证明详见解析;(2)![]() .
.
【解析】
(1)![]() 是线段
是线段![]() 的中点;连接
的中点;连接![]() ,
,![]() ,
,![]() ,证明平面
,证明平面![]() 平面
平面![]() 后即可得证;
后即可得证;
(2)建立空间直角坐标系,表示出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的坐标后,分别求出平面
的坐标后,分别求出平面![]() 的一个法向量
的一个法向量![]() 与平面
与平面![]() 的一个法向量
的一个法向量![]() ,利用
,利用![]() 即可得解.
即可得解.
(1)![]() 是线段
是线段![]() 的中点,
的中点,
证明:连接![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 是
是![]() 的中点,
的中点,![]()
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
又![]() 底面
底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]()
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() .
.
(2)![]() 平面
平面![]() 平面
平面![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,
以![]() 为原点,如图建立空间直角坐标系
为原点,如图建立空间直角坐标系![]() ,
,
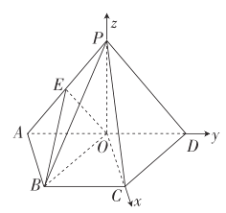
得![]() ,
,![]() ,
,![]() ,
,![]() ,
,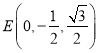 ,
,
得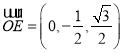 ,
,![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则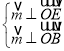 ,得
,得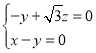 ,取
,取![]() ,
,
得![]() ,
,
又易知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,
,
则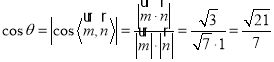 ,
,
即平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】有下列四个命题:(1)一定存在直线![]() ,使函数
,使函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称;(2)不等式:
对称;(2)不等式:![]() 的解集为
的解集为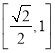 ;(3)已知数列
;(3)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则数列
,则数列![]() 一定是等比数列;(4)过抛物线
一定是等比数列;(4)过抛物线![]() 上的任意一点
上的任意一点![]() 的切线方程一定可以表示为
的切线方程一定可以表示为![]() .则正确命题的序号为_________________.
.则正确命题的序号为_________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于受到网络电商的冲击,某品牌的洗衣机在线下的销售受到影响,承受了一定的经济损失,现将![]() 地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
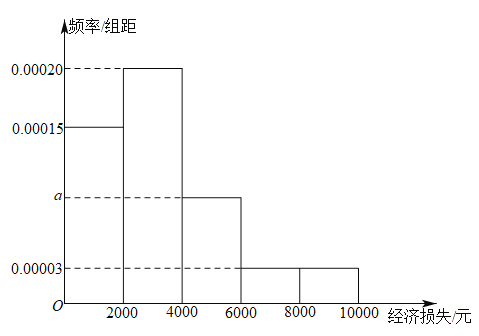
(1)求![]() 的值;
的值;
(2)求![]() 地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
(3)不经过计算,直接给出![]() 地区200家实体店经济损失的平均数
地区200家实体店经济损失的平均数![]() 与6000的大小关系.
与6000的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲对员工饮食习惯进行一次调查,从某科室的100人中的饮食结构调查结果统计如下表.
主食蔬菜 | 主食肉类 | 总计 | |
不超过45岁 | 15 | 40 | |
45岁以上 | 20 | ||
总计 |
(1)完成![]() 列联表,并判断能否有99%的把握认为员工的饮食习惯与年龄有关?
列联表,并判断能否有99%的把握认为员工的饮食习惯与年龄有关?
(2)在45岁以上员工中按照饮食习惯进行分层抽样抽出一个容量为6的样本,从这6个人中随机抽取3个人,求这3个人都主食蔬菜的概率.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足x2﹣5x+6<0.
(1)若a=1,且p∧q为真命题,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com