
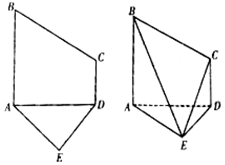
 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.分析 (1)取BC中点为N,AD中点为P,连接MN,NP,MP,可得面MNP∥面ABE,即边AB上存在这样的点N,且$\frac{BN}{BC}=\frac{1}{2}$,使得MN∥平面ABE.
(2)以A为原点,以AD为y轴,以AB为z轴建立空间直角坐标系.则A(0,0,0),B(0,0,4),$C({0,2\sqrt{2},2})$,$D({0,2\sqrt{2},0})$,$E({\sqrt{2},\sqrt{2},0})$.利用向量法求解.
解答 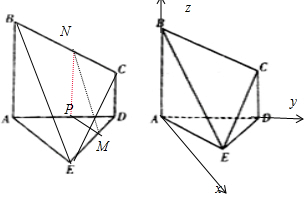 解:(1)证明:取BC中点为N,AD中点为P,
解:(1)证明:取BC中点为N,AD中点为P,
连接MN,NP,MP.∵AE∥PM,AE⊆面ABE,MP?面ABE∴PM∥面ABE,
同理PN∥面ABE,又MP∩NP=P∴面MNP∥面ABE.
∴边AB上存在这样的点N,且$\frac{BN}{BC}=\frac{1}{2}$,使得MN∥平面ABE.
(2)以A为原点,以AD为y轴,以AB为z轴建立空间直角坐标系.
则A(0,0,0),B(0,0,4),$C({0,2\sqrt{2},2})$,$D({0,2\sqrt{2},0})$,$E({\sqrt{2},\sqrt{2},0})$.
∵DE⊥AE,DE⊥AB∴DE⊥面ABE∴面ABE的一个法向量为$\overrightarrow{DE}=({\sqrt{2},-\sqrt{2},0})$
设面BCE的一个法向量为$\overrightarrow n=({x,y,z})$∵$\overrightarrow{BC}=({0,2\sqrt{2},-2})$,$\overrightarrow{BE}=({\sqrt{2},\sqrt{2},-4})$.
∴$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BC}=2\sqrt{2}y-2z=0\\ \overrightarrow n•\overrightarrow{BE}=\sqrt{2}x+\sqrt{2}y-4z=0\end{array}\right.$令y=1,则x=3,$z=\sqrt{2}$∵$\overrightarrow n=({3,1,\sqrt{2}})$.
∴$cos\left?{\overrightarrow{DE},\overrightarrow n}\right>=\frac{{\overrightarrow{DE}•\overrightarrow n}}{{|{\overrightarrow{DE}}||{\overrightarrow n}|}}$=$\frac{{2\sqrt{2}}}{{2×2\sqrt{3}}}=\frac{{\sqrt{6}}}{6}$.
∴二面角A-BE-C的平面角的余弦值为$-\frac{{\sqrt{6}}}{6}$.
点评 本题考查了空间线面平行的判定,存在性问题,向量法求二面角,属于中档题,


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{7}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5] | B. | (-∞,5] | C. | {1,2,3,4,5} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB、BB1的中点,AB=BC.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB、BB1的中点,AB=BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com