
| A. | $\frac{3}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{9}$ |
分析 设已知第一次取出的是白球为事件A,第二次也取到白球为事件B,先求出P(AB)的概率,然后利用条件概率公式进行计算即可.
解答 解:设已知第一次取出的是白球为事件A,第二次也取到白球为事件B.
则由题意知,P(A)=$\frac{4}{6}$=$\frac{2}{3}$,P(AB)=$\frac{4×3}{6×5}$=$\frac{2}{5}$,
所以已知第一次取出的是白球,则第二次也取到白球的概率为P(B|A)=$\frac{\frac{2}{5}}{\frac{2}{3}}$=$\frac{3}{5}$.
故选:A.
点评 本题主要考查条件概率的求法,熟练掌握条件概率的概率公式是关键.


科目:高中数学 来源: 题型:填空题
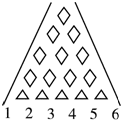 某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为$\frac{5}{16}$.
某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果某人在该游戏中,猜得珠子从3号口出来,那么他取胜的概率为$\frac{5}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,5} | B. | {1,2,4,5} | C. | {1,5} | D. | {2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{2}$ | B. | ±1 | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线段 | B. | 直线 | C. | 圆 | D. | 射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com