
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() (
(![]() )成等差数列,若存在,求出所有满足条件的
)成等差数列,若存在,求出所有满足条件的![]() ,
,![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)不存在
(3)不存在
【解析】
试题(1)先根据和项与通项关系得项之间递推关系式,再根据等比数列定义以及通项公式求数列![]() 通项公式;对条件
通项公式;对条件![]() 变形得
变形得![]() ,再根据等差数列定义以及通项公式求数列
,再根据等差数列定义以及通项公式求数列![]() 通项公式;(2)先根据错位相减法得
通项公式;(2)先根据错位相减法得![]() ,再参变分离得
,再参变分离得![]() 恒成立,利用数列单调性可得
恒成立,利用数列单调性可得![]() 最小值,即得实数
最小值,即得实数![]() 的取值范围.(3)先根据等差数列性质得
的取值范围.(3)先根据等差数列性质得![]() ,再利用奇偶分析法讨论解的情况
,再利用奇偶分析法讨论解的情况
试题解析:(1)当![]() 时,
时,![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
两式相减得![]() ,又
,又![]() ,所以
,所以![]() ,
,
从而数列![]() 为首项
为首项![]() ,公比
,公比![]() 的等比数列,
的等比数列,
从而数列![]() 的通项公式为
的通项公式为![]() .
.
由![]() 两边同除以
两边同除以![]() ,得
,得![]() ,
,
从而数列![]() 为首项
为首项![]() ,公差
,公差![]() 的等差数列,所以
的等差数列,所以![]() ,
,
从而数列![]() 的通项公式为
的通项公式为![]() .
.
(2)由(1)得![]() ,
,
于是![]() ,
,
所以![]() ,
,
两式相减得![]() ,
,
所以![]() ,
,
由(1)得![]() ,
,
因为对![]()
![]() ,都有
,都有![]() ,即
,即![]() 恒成立,
恒成立,
所以![]() 恒成立,
恒成立,
记![]() ,
,
所以![]() ,
,
因为![]()
![]() ,从而数列
,从而数列![]() 为递增数列,
为递增数列,
所以当![]() 时,
时,![]() 取最小值
取最小值![]() ,于是
,于是![]() .
.
(3)假设存在正整数![]() ,使
,使![]() (
(![]() )成等差数列,则
)成等差数列,则![]() ,
,
即![]() ,
,
若![]() 为偶数,则
为偶数,则![]() 为奇数,而
为奇数,而![]() 为偶数,上式不成立.
为偶数,上式不成立.
若![]() 为奇数,设
为奇数,设![]() ,则
,则![]() ,
,
于是![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 与
与![]() 矛盾;
矛盾;
当![]() 时,上式左边为奇数,右边为偶数,显然不成立.
时,上式左边为奇数,右边为偶数,显然不成立.
综上所述,满足条件的![]() 不存在.
不存在.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】随着移动支付的普及,中国人的生活方式正在悄然发生改变,带智能手机而不带钱包出门渐渐成为中国人的新习惯.在调查“现金支付,银联卡支付,手机支付”三种支付方式中“最常用的支付方式”这个问题时,在中国某地,从20岁到40岁人群中随机抽取55人,从40岁到60岁人群随机抽取45人,进行答题.20岁到40岁人群的支付情况是选择现金支付的占![]() 、银联卡支付的占
、银联卡支付的占![]() 、手机支付的占
、手机支付的占![]() .40岁到60岁人群的支付情况是:现金支付的占
.40岁到60岁人群的支付情况是:现金支付的占![]() 、银联卡支付的占
、银联卡支付的占![]() 、手机支付的占
、手机支付的占![]() .
.
(1)请根据以上调查结果将下面![]() 列联表补充完整;并判断至多有多少把握认为支付方式与年龄有关;
列联表补充完整;并判断至多有多少把握认为支付方式与年龄有关;
手机支付 | 其他支付方式 | 合计 | |
20岁到40岁 | |||
40岁到60岁 | |||
合计 |
(2)商家为了鼓励使用手机支付规定手机支付打9折,其他支付方式不打折.现有一物品售价100元,以样本中支付方式的频率估计一件产品支付方式的概率,假设购买每件物品的支付方式相互独立.求4件此种物品销售额的数学期望.
附:![]() ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.01 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.636 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | y | m |
非单车用户 | x | 32 | 70 |
合计 | n | 50 | 100 |
(1)求出列联表中字母x、y、m、n的值;
(2)①从此样本中,对单车用户按年龄采取分层抽样的方法抽出5人进行深入调研,其中不小于40岁的人应抽多少人?
②从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数![]() 的不足近似值和过剩近似值分别为
的不足近似值和过剩近似值分别为![]() 和
和![]() ,则
,则![]() 是
是![]() 的更为精确的不足近似值或过剩近似值.我们知道
的更为精确的不足近似值或过剩近似值.我们知道![]() ,若令
,若令![]() ,则第一次用“调日法”后得
,则第一次用“调日法”后得![]() 是
是![]() 的更为精确的过剩近似值,即
的更为精确的过剩近似值,即![]() ,若每次都取最简分数,那么第四次用“调日法”后可得
,若每次都取最简分数,那么第四次用“调日法”后可得![]() 的近似分数为( )
的近似分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级体育课进行一次篮球定点投篮测试,规定每人最多投3次,每次投篮的结果相互独立.在![]() 处每投进一球得3分,在
处每投进一球得3分,在![]() 处每投进一球得2分,否则得0分.将学生得分逐次累加并用
处每投进一球得2分,否则得0分.将学生得分逐次累加并用![]() 表示,如果
表示,如果![]() 的值不低于3分就判定为通过测试,立即停止投篮,否则应继续投篮,直到投完三次为止.现有两种投篮方案:方案1:先在
的值不低于3分就判定为通过测试,立即停止投篮,否则应继续投篮,直到投完三次为止.现有两种投篮方案:方案1:先在![]() 处投一球,以后都在
处投一球,以后都在![]() 处投;方案2:都在
处投;方案2:都在![]() 处投篮.已知甲同学在
处投篮.已知甲同学在![]() 处投篮的命中率为
处投篮的命中率为![]() ,在
,在![]() 处投篮的命中率为
处投篮的命中率为![]() .
.
(1)若甲同学选择方案1,求他测试结束后所得总分![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABED中,AB//DE,AB![]() BE,点C在AB上,且AB
BE,点C在AB上,且AB![]() CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE
CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE![]() .
.
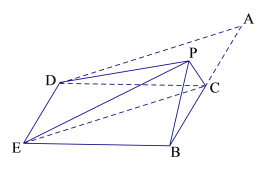
(1)求证:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱锥P-EBC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com