
【题目】已知直线![]() 过点
过点![]() 和椭圆
和椭圆![]() :
:![]() 的焦点且方向向量为
的焦点且方向向量为![]() ,且椭圆
,且椭圆![]() 的中心关于直线
的中心关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() 、
、![]() ,且满足
,且满足![]() (
(![]() 为原点)?若存在,求直线
为原点)?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的两焦点与短轴两端点围成面积为12的正方形.
)的两焦点与短轴两端点围成面积为12的正方形.
(1)求椭圆C的标准方程;
(2)我们称圆心在椭圆上运动,半径为![]() 的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线
的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,当
,当![]() 时,求此时“卫星圆”的个数.
时,求此时“卫星圆”的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双11”促销活动中,某商场为了吸引顾客,搞好促销活动,采用“双色球”定折扣的方式促销,即:在红、黄的两个纸箱中分别装有大小完全相同的红、黄球各5个,每种颜色的5个球上标有1,2,3,4,5等5个数字,顾客结账时,先分别从红、黄的两个纸箱中各取一球,按两个球的数字之和为折扣打折,如![]() ,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
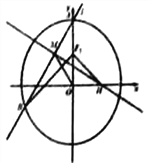
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点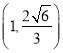 .
.
(1)求椭圆![]() 的方程.
的方程.
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4﹣2a1,S11=11b4.
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{anbn}的前n项和为Tn(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com