
【题目】某单位有员工1000名,平均每人每年创造利润10万元,为了增加企业竞争力,决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业,调整后这
)名员工从事第三产业,调整后这![]() 名员工他们平均每人创造利润为
名员工他们平均每人创造利润为![]() 万元,剩下的员工平均每人每年创造的利润可以提高
万元,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整多少名员工从事第三产业?
(2)设![]() ,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求
,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求![]() 的最大值.
的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 在
在![]() 上有定义,实数
上有定义,实数![]() 和
和![]() 满足
满足![]() ,若
,若![]() 在区间
在区间![]() 上不存在最小值,则称
上不存在最小值,则称![]() 在
在![]() 上具有性质
上具有性质![]() .
.
(1)当![]() ,且
,且![]() 在区间
在区间![]() 上具有性质
上具有性质![]() 时,求常数
时,求常数![]() 的取值范围;
的取值范围;
(2)已知![]() (
(![]() ),且当
),且当![]() 时,
时,![]() ,判别
,判别![]() 在区间
在区间![]() 上是否具有性质
上是否具有性质![]() ,试说明理由.
,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为正方体ABCD-A1B1C1D1,动点M从B1点出发,在正方体表面沿逆时针方向运动一周后,再回到B1的运动过程中,点M与平面A1DC1的距离保持不变,运动的路程x与l=MA1+MC1+MD之间满足函数关系l=f(x),则此函数图象大致是( )
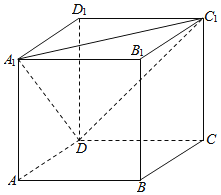
A. 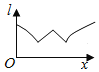 B.
B. 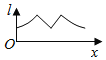
C. 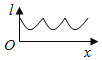 D.
D. 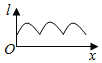
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.
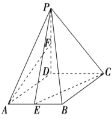
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的方程为
的方程为![]() ,其中常数
,其中常数![]() ,
,![]() 是抛物线
是抛物线![]() 的焦点.
的焦点.
(1)若直线![]() 被抛物线
被抛物线![]() 所截得的弦长为6,求
所截得的弦长为6,求![]() 的值;
的值;
(2)设![]() 是点
是点![]() 关于顶点
关于顶点![]() 的对称点,
的对称点,![]() 是抛物线
是抛物线![]() 上的动点,求
上的动点,求![]() 的最大值;
的最大值;
(3)设![]() ,
,![]() 、
、![]() 是两条互相垂直,且均经过点
是两条互相垂直,且均经过点![]() 的直线,
的直线,![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() ,若点
,若点![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)在(1)的条件下,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列,求
)依次成等差数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】贺先生想向银行贷款买辆新能源车,银行可以贷给贺先生N元,一年后需要一次性还1.02N元.
(1)贺先生发现一个投资理财方案:每个月月初投资![]() 元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12
元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12![]() 元,按投资方案投资,求
元,按投资方案投资,求![]() 的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
(2)贺先生又发现一个投资方案:第![]() 个月月初投资
个月月初投资![]() 元
元![]() 共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
(参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com