
【题目】已知椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() 右焦点为
右焦点为![]() ,直线
,直线![]() 是椭圆
是椭圆![]() 在点
在点![]() 处的切线.设点
处的切线.设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,且当
,且当![]() 时,
时, ![]() 是等腰三角形.
是等腰三角形.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设椭圆![]() 的长轴长等于
的长轴长等于![]() ,当点
,当点![]() 运动时,试判断以
运动时,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
【答案】(1)![]() (2)以
(2)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
解:(Ⅰ)根据题意,得直线![]() 与
与![]() 轴垂直,
轴垂直,
![]() 当
当![]() 时,
时, ![]() 是等腰三角形.
是等腰三角形.
![]()
![]()
![]()
![]()
(Ⅱ)以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系是相切,证明如下:
的位置关系是相切,证明如下:
![]() 椭圆C的长轴长等于
椭圆C的长轴长等于![]() ,
,
![]()
根据(Ⅰ),得椭圆的标准方程为: ![]() ,
,
设直线![]() 的方程为:
的方程为: ![]() ,
,
则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() ,
,
联立方程组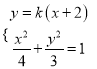 ,消去
,消去![]() ,并整理,得
,并整理,得
![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则
,则
![]()
![]()
因为点![]() ,
,
(ⅰ)当![]() 时,点
时,点![]() 坐标为
坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,此时,以
,此时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切;
相切;
(ⅱ)当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为:
的方程为: ![]() ,
,
![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为 ,
,
![]() ,
,
![]() 以
以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
【解析】试题分析:(Ⅰ)根据题意,结合给定的条件,得到![]() ,然后确定其离心率即可;
,然后确定其离心率即可;
(Ⅱ)设直线![]() 的方程为:
的方程为: ![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() ,
,
联立方程组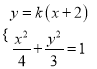 ,消去
,消去![]() ,并整理,得
,并整理,得![]() ,
,
分情况进行讨论,结合直线与圆相切的条件进行判断即可.
试题解析:(Ⅰ)根据题意,得直线![]() 与
与![]() 轴垂直,
轴垂直,
![]() 当
当![]() 时,
时, ![]() 是等腰三角形.
是等腰三角形.
![]()
![]()
![]()
![]()
(Ⅱ)以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系是相切,证明如下:
的位置关系是相切,证明如下:
![]() 椭圆C的长轴长等于
椭圆C的长轴长等于![]() ,
,
![]()
根据(Ⅰ),得椭圆的标准方程为: ![]() ,
,
设直线![]() 的方程为:
的方程为: ![]() ,
,
则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() ,
,
联立方程组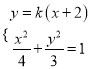 ,消去
,消去![]() ,并整理,得
,并整理,得
![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则
,则
![]()
![]()
因为点![]() ,
,
(ⅰ)当![]() 时,点
时,点![]() 坐标为
坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,此时,以
,此时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切;
相切;
(ⅱ)当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为:
的方程为: ![]() ,
,
![]() ,
,
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为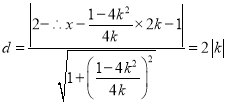 ,
,
![]() ,
,
![]() 以
以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)求圆心C的坐标及半径r的大小;
(2)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l的方程;
(3)从圆外一点![]() 向圆引一条切线,切点为M,O为坐标原点,且
向圆引一条切线,切点为M,O为坐标原点,且![]() ,求点P的轨迹方程.
,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扎比瓦卡是2018年俄罗斯世界杯足球赛吉祥物,该吉祥物以西伯利亚平原狼为蓝本.扎比瓦卡,俄语意为“进球者”.某厂生产“扎比瓦卡”的固定成本为15000元,每生产一件“扎比瓦卡”需要增加投入20元,根据初步测算,每个销售价格满足函数 ,其中x是“扎比瓦卡”的月产量(每月全部售完).
,其中x是“扎比瓦卡”的月产量(每月全部售完).
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,该厂所获利润最大?最大利润是多少?(总收益=总成本+利润).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x![]() )+a的最大值为2.
)+a的最大值为2.
(1)求实数a的值;
(2)在给定的直角坐标系上作出函数f(x)在[0,π]上的图象:
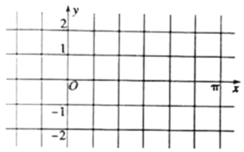
(3)求函数f(x)在[![]() ,
,![]() ]上的零点,
]上的零点,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,侧面
的菱形,侧面![]() 底面
底面![]() ,
,![]() ,
, ![]() ,
, ![]() 是
是![]() 中点,点
中点,点![]() 在侧棱
在侧棱![]() 上.
上.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 是
是![]() 中点,求二面角
中点,求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)是否存在![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
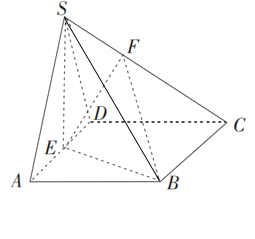
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com