
【题目】某部门经统计,客户对不同款型理财产品的最满意程度百分比和对应的理财总销售量(万元)如下表(最满意度百分比超高时总销售量最高):
产品款型 | A | B | C | D | E | F | G | H | I | J |
最满意度% | 20 | 34 | 25 | 19 | 26 | 20 | 19 | 24 | 19 | 13 |
总销量(万元) | 80 | 89 | 89 | 78 | 75 | 71 | 65 | 62 | 60 | 52 |
设![]() 表示理财产品最满意度的百分比,
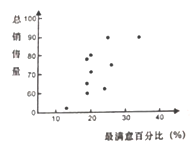
表示理财产品最满意度的百分比,![]() 为该理财产品的总销售量(万元).这些数据的散点图如图所示.
为该理财产品的总销售量(万元).这些数据的散点图如图所示.
(1)在![]() 份
份![]() 款型理财产品的顾客满意度调查资料中任取
款型理财产品的顾客满意度调查资料中任取![]() 份;只有一份最满意的,求含有最满意客户资料事件的概率.
份;只有一份最满意的,求含有最满意客户资料事件的概率.
(2)我们约定:相关系数的绝对值在![]() 以下是无线性相关,在
以下是无线性相关,在![]() 以上(含
以上(含![]() )至
)至![]() 是一般线性相关,在
是一般线性相关,在![]() 以上(含
以上(含![]() )是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到
)是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到![]() ).
).
数据参考计算值:
项目 |
|
|
|
|
|
|
值 | 21.9 | 72.1 | 288.9 | 37.16 | 452.1 | 17.00 |
附:回归直线方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:
线性相关系数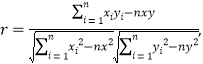
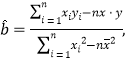
![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由最满意度表可知在![]() 份
份![]() 款型产品客户资料有最满意客户资料
款型产品客户资料有最满意客户资料![]() 份,利用列举法和古典概型概率计算公式,计算出含有最满意客户资料事件的概率.(2)根据线性相关系数公式计算出
份,利用列举法和古典概型概率计算公式,计算出含有最满意客户资料事件的概率.(2)根据线性相关系数公式计算出![]() ,故即
,故即![]() 与
与![]() 具有一般线性关系,没有达到较强的线性相关. 末位剔除数据后,利用剩下数据,根据回归直线方程计算公式,计算出回归直线方程.
具有一般线性关系,没有达到较强的线性相关. 末位剔除数据后,利用剩下数据,根据回归直线方程计算公式,计算出回归直线方程.
由最满意度表可知在![]() 份
份![]() 款型产品客户资料有最满意客户资料
款型产品客户资料有最满意客户资料![]() 份;把最满意客户资料记为
份;把最满意客户资料记为![]() ;其余客户资料记为
;其余客户资料记为![]() .
.
则任取二份资料的基本事件有: ![]()
![]()
![]() 共
共![]() 件.
件.
含有![]() 的基本事件有:
的基本事件有:![]() 共
共![]() 件.
件.
则含有最满意客户资料事件的概率为![]() ,得
,得![]()
故在这款型客户资料中任取位客户资料含有最满意客户资料事件的概率为![]() .
.
(2)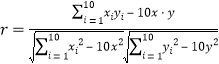
![]()
即![]() 与
与![]() 具有一般线性关系,没有达到较强的线性相关
具有一般线性关系,没有达到较强的线性相关
由末位剔除制度可知,应剔除款型
重新计算得![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
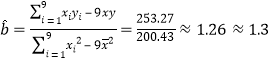
![]()
![]()
![]()
所求线性回归方程为![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知两直线方程![]() 与
与![]() ,点
,点![]() 在
在![]() 上运动,点
上运动,点![]() 在
在![]() 上运动,且线段
上运动,且线段![]() 的长为定值
的长为定值![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求原点
,求原点![]() 的直线
的直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 为
为![]() 中点,侧棱
中点,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 上的动点,且
上的动点,且![]() .
.
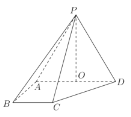
(1)求证:![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积取最大值时,求
的体积取最大值时,求![]() 到平面
到平面![]() 的距离;
的距离;
(3)在(2)的条件下求![]() 与平面
与平面![]() 所成角.
所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示多面体![]() ,其底面
,其底面![]() 为矩形且
为矩形且![]() ,四边形
,四边形![]() 为平行四边形,点
为平行四边形,点![]() 在底面
在底面![]() 内的投影恰好是
内的投影恰好是![]() 的中点.
的中点.
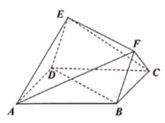
(1)已知![]() 为线段
为线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)若二面角![]() 大小为
大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解某产品的获利情况,将今年1至7月份的销售收入![]() (单位:万元)与纯利润
(单位:万元)与纯利润![]() (单位:万元)的数据进行整理后,得到如下表格:
(单位:万元)的数据进行整理后,得到如下表格:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
纯利润 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
该公司先从这7组数据中选取5组数据求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
(1)求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程(精确到0.01);
的线性回归方程(精确到0.01);
(2)若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元,则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想?
参考公式:![]() ,
,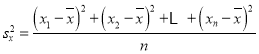 ,
,![]() ,
,![]() ;参考数据:
;参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() .以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线
.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() ,从原点O作射线交
,从原点O作射线交![]() 于点M,点N为射线OM上的点,满足
于点M,点N为射线OM上的点,满足![]() ,记点N的轨迹为曲线C.
,记点N的轨迹为曲线C.
(Ⅰ)求出直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(Ⅱ)设直线![]() 与曲线C交于P,Q两点,求
与曲线C交于P,Q两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com